Classification Metrics

Classification Metrics: 분류 성능 지표

Kaggle Classification 의 Evaluation 에 자주 사용되는 ROC-AUC를 정리해보면서, 이번 기회에 분류모델에서 자주 사용되는 성능지표(Metric)을 간단하게 정리해봅니다.

Confusion Matrix 에서 비롯되는 Metric 들은 이를 이미지로 기억하는 것이 효율적입니다.

Confusion Matrix

confusion matrix 는 해당 데이터의 정답 클래스(y_true) 와 모델의 예측 클래스(y_pred)의 일치 여부를 갯수로 센 표입니다. 주로, 정답 클래스는 행으로(row), 예측 클래스는 열로(columns) 표현합니다.

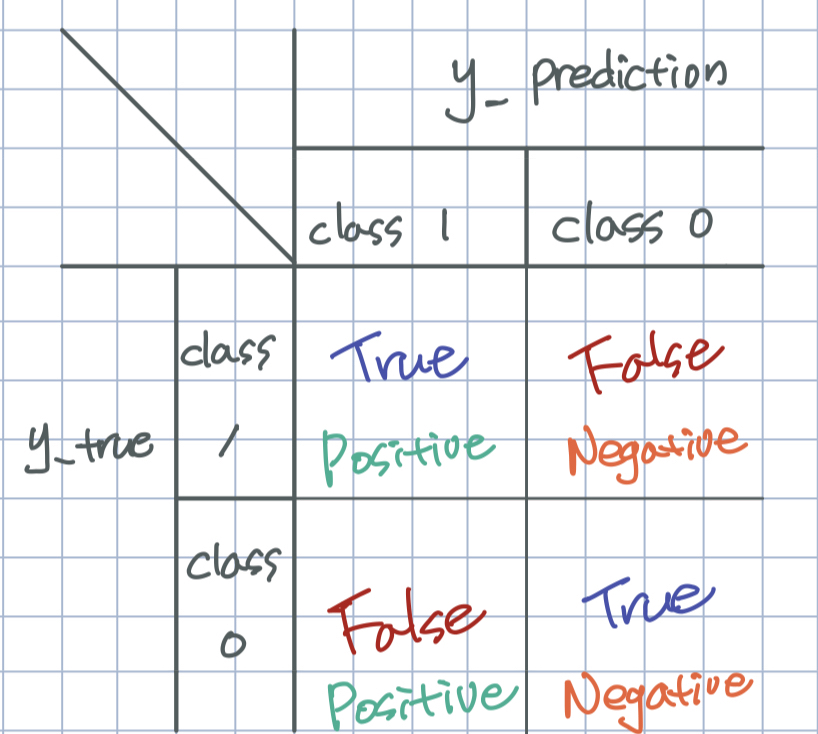
• (정의하기에 따라 다르지만) 일반적으로, class 1 을 positive로, class 0 을 negative 로 표기합니다.
• 우리가 예측한 클래스를 기준으로 Positive 와 Negative 를 구분합니다.
• 그리고 정답과 맞았는지, 틀렸는지를 알려주기 위해 True 와 False 를 각각 붙여줍니다.

Accuracy: 정확도

• 전체 데이터에 대해 맞게 예측한 비율

$$
\frac{TP+TN}{TP+FN+FP+TN}
$$

Precision: 정밀도

• class 1 이라고 예측한 데이터 중, 실제로 class 1 인 데이터의 비율

$$\frac{TP}{TP+FP}$$

우리의 모델이 기본적인 decision이 class 0 이라고 생각할 때, class 1 은 특별한 경우를 detect 한 경우 일 것입니다. 이 때 class 1 이라고 알람을 울리는 우리의 모델이 얼마나 세밀하게 class를 구분 할 수 있는지의 정도를 수치화 한 것입니다.

Recall: 재현율

• 실제로 class 1 인 데이터 중에 class 1 이라고 예측한 비율
• = Sensivity = TPR

$$\frac{TP}{TP+FN}$$

제가 기억하는 방식은, 자동차에 결함이 발견되서 recall 이 되어야 하는데 (실제 고장 데이터중) 얼마나 recall 됐는지로 생각합니다.

Fall-out: 위양성율

• 실제로 class 1 이 아닌 데이터 중에 class 1이라고 예측한 비율
• 낮을 수록 좋음
• = FPR = 1 - Specificity
• Specificity = 1 - Fall out

$$\frac{FP}{FP+TN}$$

실제로 양성데이터가 아닌 데이터에 대해서 우리의 모델이 양성이라고 잘못 예측한 비율을 말합니다. 억울한 데이터의 정도를 측정했다고 생각 할 수 있습니다.

각 Metric 간의 상관관계

우리 모델의 decision function 을 f(x) 라 할 때, 우리는 f(x)의 결과와 threshold (decision point)를 기준으로 class를 구분합니다.

• Recall vs Fall-out : 양의 상관관계

  Recall은 위의 정의에 의하듯이, 실제로 positive 인 클래스에 대해 얼마나 positve 라고 예측했는지의 비율입니다. 우리가 Recall 을 높이기 위해서는 고정되어있는 실제 positive 데이터 수에 대해 예측하는 positive 데이터의 갯수 threshold 를 낮춰 늘리면 됩니다. 이에 반해 threshold 를 낮추게 되면, 실제로 positive 가 아닌 데이터에 대해 positive 라고 예측하는 억울한 데이터가 많아지므로 Fall-out 은 커지게 되고 둘은 양의 상관관계를 갖게 됩니다.

• Recall vs Precision : 대략적인 음의 상관관계

  위에 설명한 것처럼 threshold 를 낮춰 우리가 예측하는 positive 클래스의 숫자를 늘리게 되면, recall 은 높아지는 반면, 예측한 positive 데이터 중 실제 positive 데이터의 비율은 작아 질 수 있습니다.

F-beta score

• precision 과 recall의 가중 조화평균

$$(\frac{1}{1+\beta^2}\frac{1}{precision} + \frac{\beta^2}{1+\beta^2}\frac{1}{recall})^{-1}$$

이처럼, 다양한 Metric 에 대해 우리가 초점을 맞추는 것에 따라 모델의 성능은 다르게 바라 볼 수 있습니다. 따라서 모델에 대해 성능을 평가하고 최종 모델을 선택함에 있어, 서로 다른 Metric 을 동시에 비교해야합니다. 이를 위해 precision 과 recall 을 precision 에 beta^2 만큼 가중하여 바라보는 스코어가 F beta score 입니다.

이 중 beta=1 일 때, score 가 우리가 자주 보는 f1 score 입니다.

$$F_1=\frac{2precisionrecall}{precision+recall}$$

ROC Curve: Receiver Operator Characteristic Curve

• Recall vs Fallout 의 plot (TPR vs FPR)

위의 예시 처럼, 우리가 클래스를 판별하는 기준이 되는 threshold (decision point) 를 올리거나 내리면서, recall 과 fall out 은 바뀌게 됩니다. 이렇게 threshhold 를 변화 해 가면서, recall 과 fall out 을 plotting 한 것이 ROC curve 입니다.

• sklearn.metrics.roc_curve() 의 documentation

(ROC-)AUC: Area Under Curve

• 위에서 그린 ROC Curve 의 넓이를 점수로써 사용하는 것이 AUC 입니다. AUC 의 유의미한 범위는 class 를 50%의 확률로 random 하게 예측한 넓이인 0.5 보다는 클 것이고, 가장 최대의 AUC 의 넓이는 1 일 것이므로 0.5≤AUC≤1 의 범위를 갖는 score 입니다.

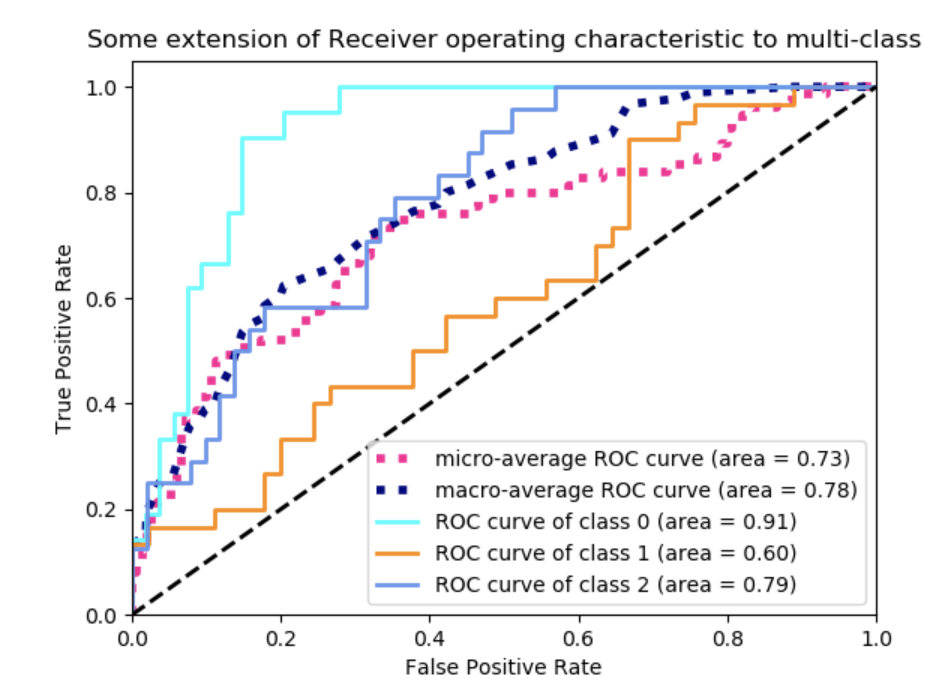
• ROC 커브와 AUC score 를 보고 모델에 대한 성능을 평가 하기 위해서, ROC 는 같은 Fall out 에 대해 Recall 은 더 높길 바라고, 같은 Recall 에 대해서는, Recall 이 더 작길 바랍니다. 결국, 그래프가 왼쪽 위로 그려지고, AUC 즉 curve 의 넓이는 커지는 것이 더 좋은 성능의 모델이라고 볼 수 있습니다.