[Study] Model-Free Prediction

본 글은 David Silver의 강의를 듣고서 정리한 글이다. 이번 강의는 model-free 구조를 살펴보는 강의이다.

model-free?

앞선 강의에서 state value를 계산하는 것들을 봤는데 이를 계산할 수 있었던 이유는 우리가 state transition probability라던지, policy라던지, reward가 어떻게 나오는지에 대한 probability를 알고 있기 때문에 가능했다.

오늘 강의에서는 우리는 주어진 environement에 대한 지식이 없고, 그저 agent가 겪게 되는 experience(episode)를 통해 주어진 environement에 대한 policy의 value를 추측하는 것이다.

prediction?

RL에서는 어느정도 evaluation과 interchangable하게 쓰이는 것 같다.

보통 policy evaluation을 prediction problem의 범주로 본다.

❗ problem의 범주는 보통 prediction, 그리고 control로 나누어진다.

오늘 배울 것들

• Monte-Carlo (MC) Policy Evaluation
• Temporal-Difference (TD) policy evaluation
• TD($\lambda$) policy evaluation =⇒ MC와 TD(0)의 사이
• MC, TD, TD($\lambda$), 그리고 DP와의 관계

Monte-Carlo policy evaluation

특징

• 에피소드들로부터 배운다. ⇒ 모델을 정확히 몰라도 괜찮다.(Model-free)
• Complete episode들로부터 배운다. (episode가 진행되는 동안에 배우는 건 안된다.)
  • 따라서 episode들은 terminate되어야 한다. (terminal state에 의해서든, 아니면 episode 최대 숫자를 통해서든)
• 여러 state transition을 겪은 reward들을 바탕으로 계산하는 평균 return을 바탕으로 value를 추정한다.

실제 evaluation 과정

• 주어진 policy에 따라 agent는 episode를 경험하게 된다.
• 이전에는 모든 경우에 수를 고려해 expected return을 구했었다면, 지금은 model에 대한 지식이 없으니 경험에 의존해서만 expected return을 구한다.

1. 일단 episode를 시작하고, 주어진 policy에 따라 action을 취하면서 reward를 얻고, 이를 통해 $G_t$를 구할 수 있다.
2. First-visit인지, Every-visit인지에 따라
   1. 어떤 state에 visit하면 해당 state의 count 값(N(s))을 올리고,
   2. visit할 당시의 $G_t$값을 S(s)에 누적해 준다.
   3. (First-visit이면 말그대로 처음 state에 도달했을 때만 위 계산을 해준다.)
3. 모든 episode에 대해 위와 같은 계산을 끝마쳐주고 난 나뒤에 N(s)와 S(s)를 통해서 평균을 내준다.

MC Example

State sequence가 다음과 같이 주어졌다고 하자. (action과 reward는 생략)

s1 → s2 → s3 → s4 → s2 → sF

여기서 s2의 state value를 구해보자.

First Visit의 경우

Gt: (s2, s3, s4, s2, sF)를 통해 return을 구한다.

N(s2)=1

Every Visit:

Gt1: (s2, s3, s4, s2, sF)을 통해 return을 구한다.

Gt2 : (s2, sF)을 통해 return을 구한다.

s(s2) = Gt1 + Gt2

V(s2) = (Gt1 + Gt2)/2

Blackjack example

솔직히 적당한 예라고는 생각되지 않지만 model-free에 대한 예제로 생각한다.

Incremental MC update

• 우리가 어떤 값들의 평균을 구할 때, 맨 마지막에 한꺼번에 구할 수도 있지만
• 이전에 구해 놓은 평균을 이용해서 구할 수 있다.

• 마찬가지로 V(S) (return들의 평균)을 구할 때도, 이전에 구해 놓은 V(S) 값과 새롭게 얻게 된 $G_t$값을 이용해 구할 수 있다.
• 아래와 같이 특정 상수($\alpha$)를 이용해서 이전에 구해놓은 평균과 새롭게 얻게 된 값을 어떤 식으로 이용할 것인지 weight를 고정해서 줄 수 있다.

Temporal-difference (TD) policy evaluation

특징

• **(MC와 동일)**에피소드들로부터 배운다. ⇒ 모델을 정확히 몰라도 괜찮다.(Model-free)
• (MC와 상이) incomplete episode들로부터 학습할 수 있다. (bootstrapping)

MC와 TD의 비교

MC

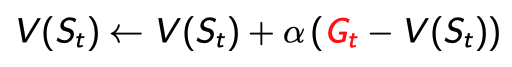
실제 complete episode를 통해 알고 있는 $G_t$를 통해 업데이트 한다.

TD(0)

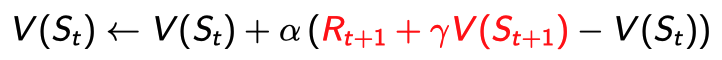
MC처럼 진짜 $G_t$값이 아닌 $G_t$의 estimator라고 할 수 있는 $R_{t+1}+\gamma V(S_{t+1})$을 사용한다.

• $V(S_{t+1})$이 최종적인 값이 아니기 때문에 estimate인 것이다.
• 예전 $V(S_{t+1})$ 값을 사용할 수 있기 때문에 꼭 episode를 complete하지 않더라도 바로바로 업데이트할 수 있다. (online)

❗ TD에서 빨간 부분은 TD 뒤에 들어가는 숫자에 따라 달라진다.

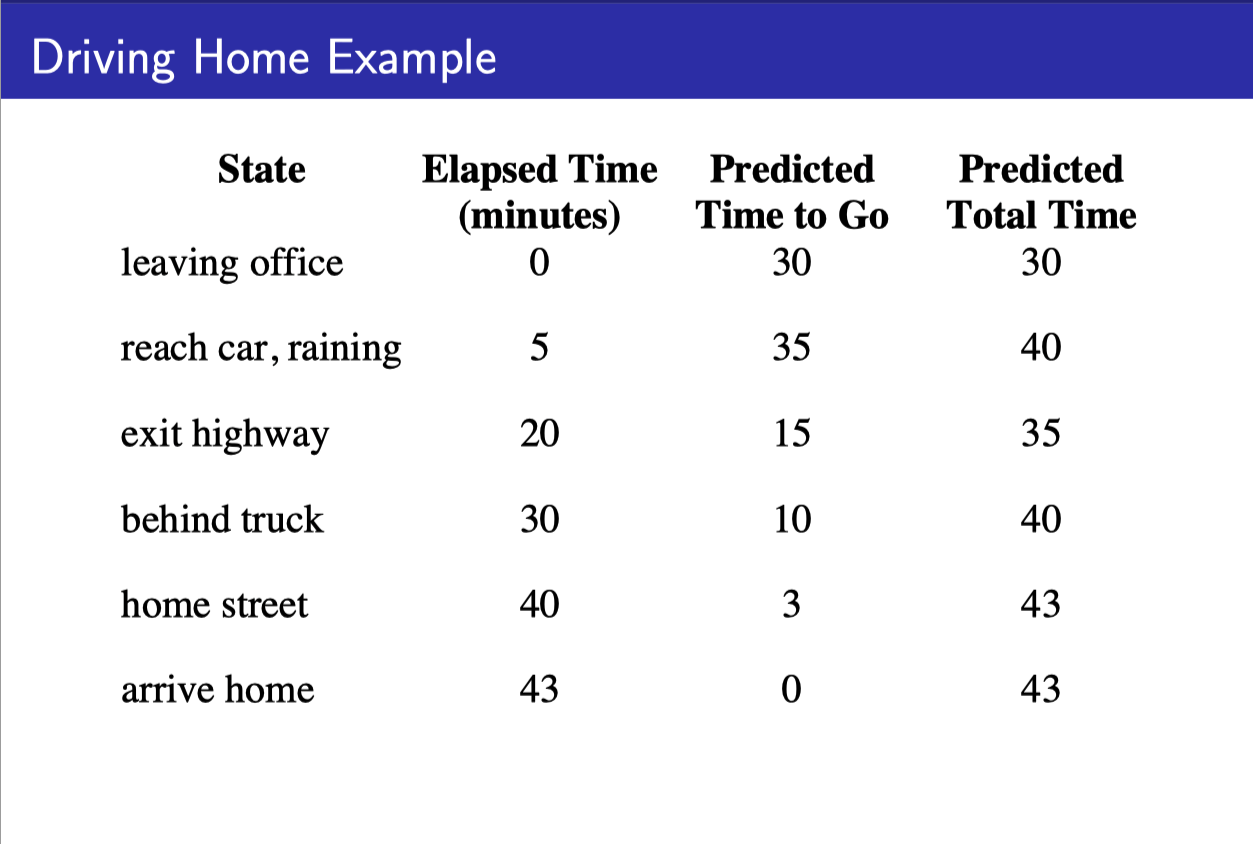
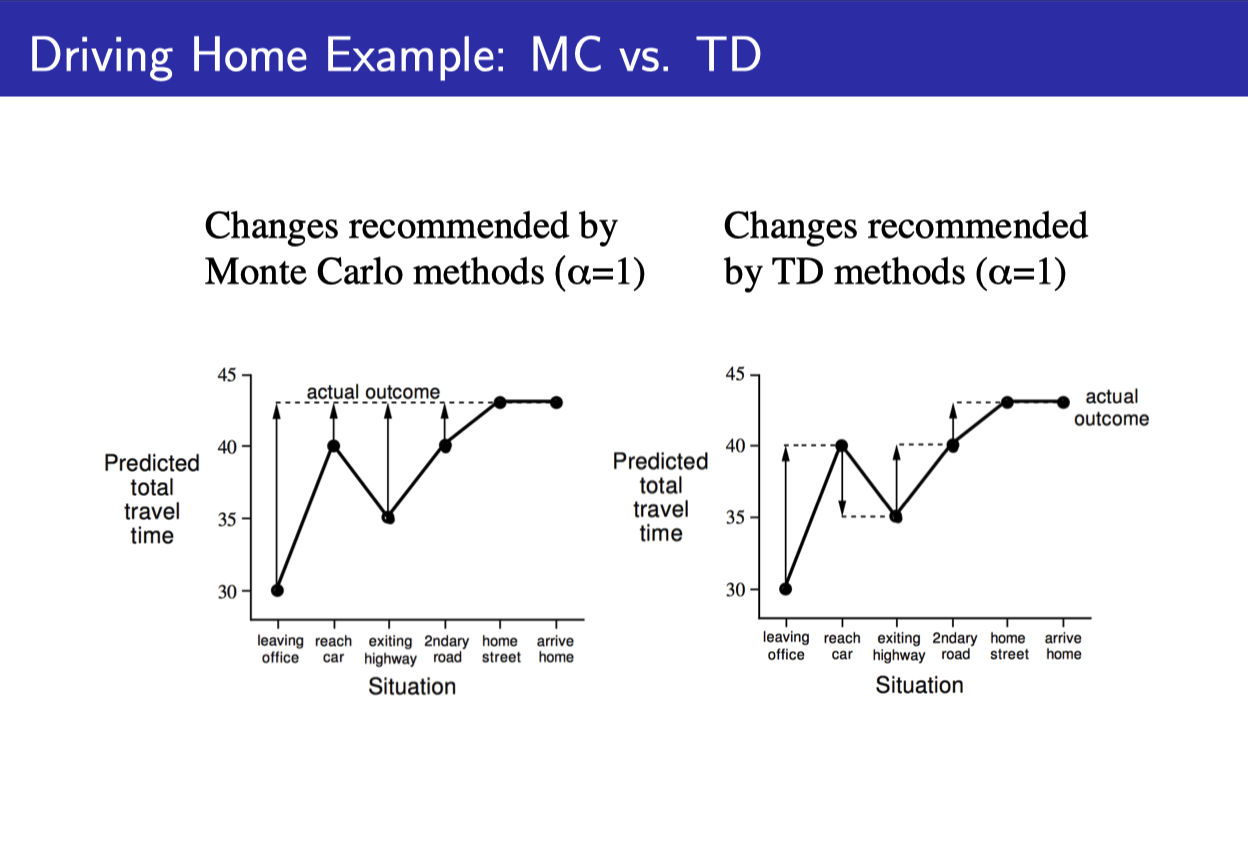
• State value를 reward가 아닌 그 state에서부터 집까지 걸리는 예상 시간이라고 하자.
• MC 같은 경우에는 다음 state에서 뭐라고 새롭게 예측했던 상관없이 처음부터 끝까지 다 가본 다음, 실제 집까지 걸린 시간과, 그 state에서 예상한 걸린 시간의 차를 가지고 계산한다.
• TD 같은 경우에는 이전 state value를 업데이트할 때, 현재 state value만을 이용해서 업데이트한다.
  • 현재 state value가 실제로 정확하던 아니던 상관이 없다. 반복하다 보면 맞아 갈테니까

MC vs TD (2)

MC

• 에피소드가 끝나서 return을 알아낼 때까지 기다려야 된다.
• terminate가 꼭 필요하다.

TD

• episode가 끝나지 않아도 매 step마다 업데이트가 가능 (online)
• 바로바로 배울 수 있으므로 꼭 episode가 끝날 필요는 없다.

MC vs TD (3) - Bias/Variance

MC

• $G_t$=unbiased estimate of $v_{\pi}(S_t)$
• Zero bias
• $G_t$는 뒤에 많은 random variable이 따라오므로 variance가 높다.
• initial value에 덜 sensitive하다.

TD

• “True” TD target = $R_{t+1}+\gamma v_\pi (S_{t+1})$=unbiased estimate of $v_\pi (S_t)$
• TD target = $R_{t+1}+\gamma V (S_{t+1})$=biased estimate of $v_\pi (S_t)$
• TD target은 한가지 action값과 이미 정해진 V값에만 의존하므로 variance가 낮다.
• intial value에 sensitive하다.

Random walk example

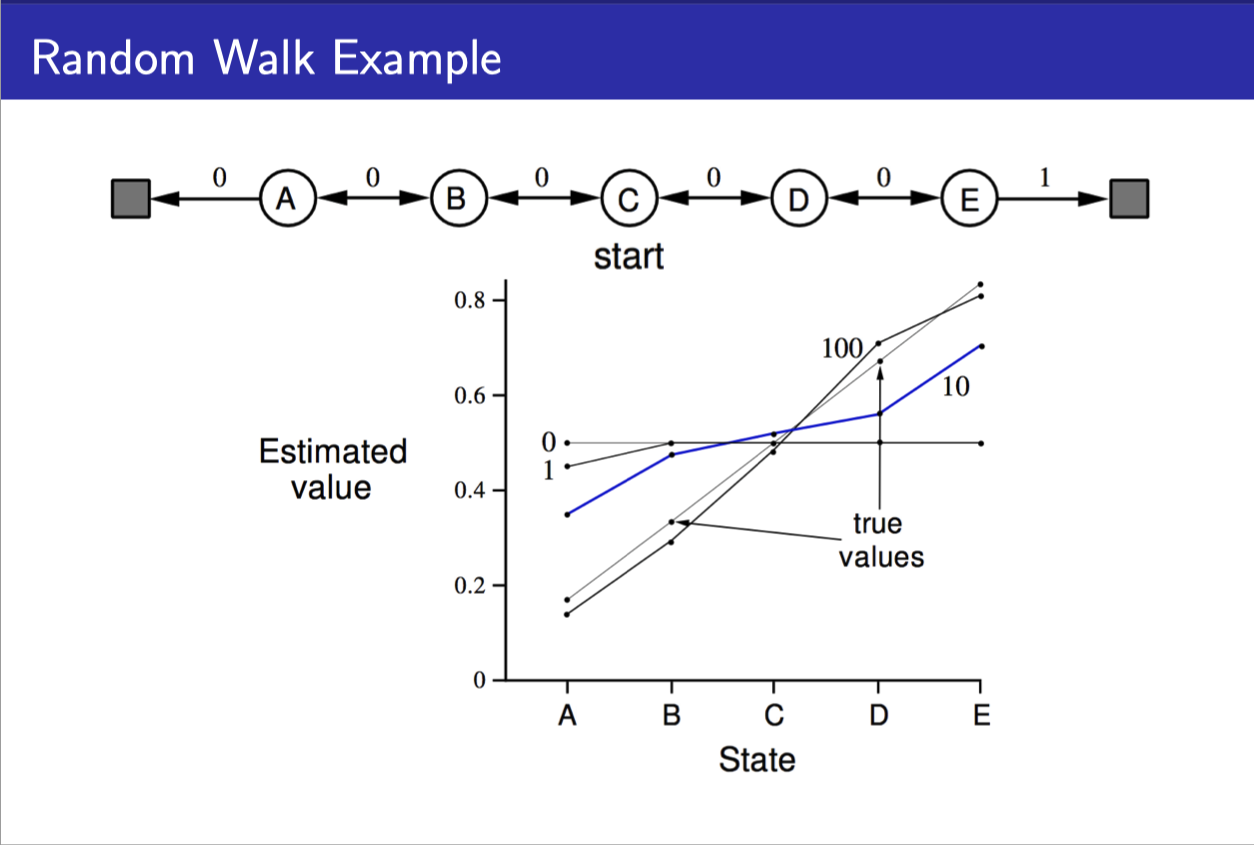
• 처음에 0.5로 value들이 initialize되어 있다가
• 계속 episode가 늘어날수록 true value(아마도 DP로 구했을 법한)로 수렴하는 것을 볼 수 있다.

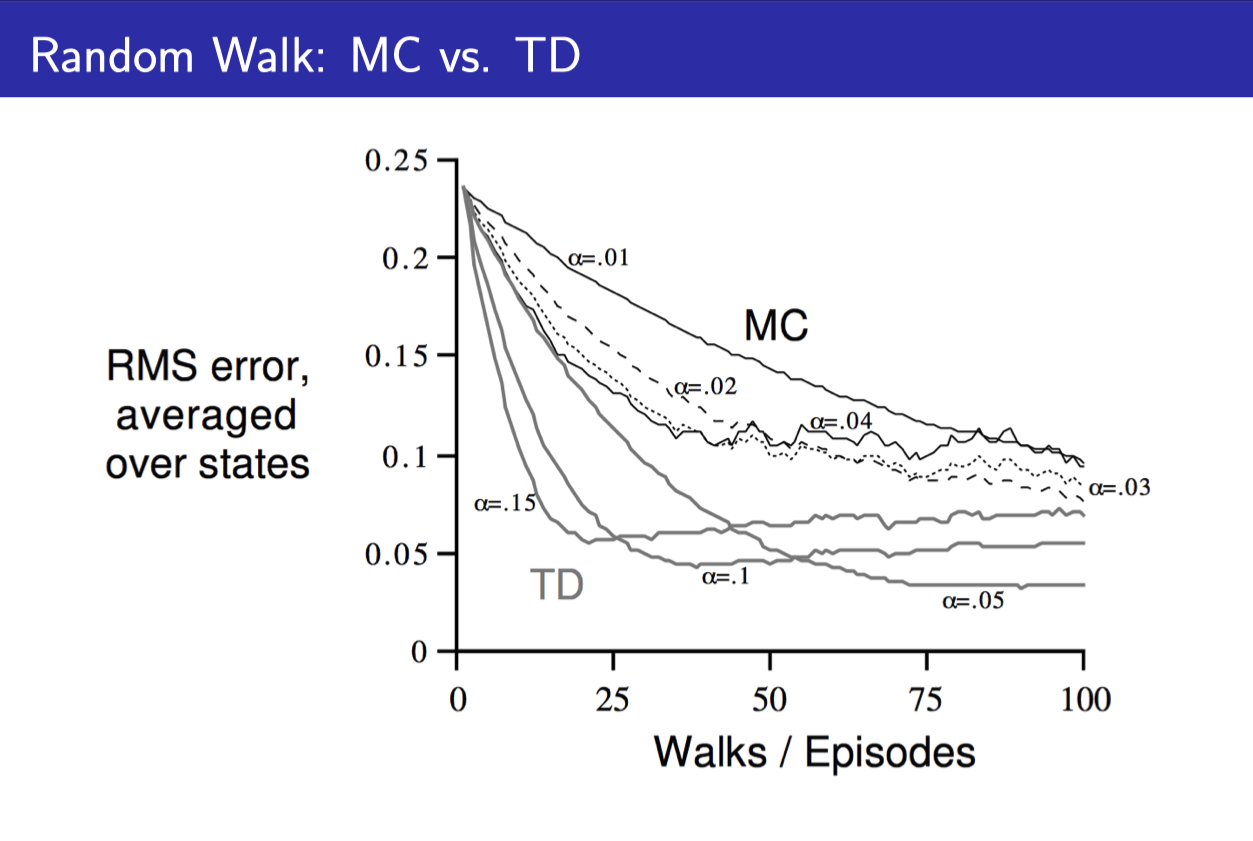
• TD가 MC보다 더 빠르게 True value에 접근하는 것을 볼 수 있다.

Batch MC and TD

• episode를 무한히 많이 늘리면 V(s)가 $v_{\pi}(s)$에 가까워 지겠지만 실제로는 그렇게 할 수 없다.
• 그래서 finite한 k개의 episode 중에서 계속 sample해서 MC나 TD를 시행한다.

AB example

• 보면 A의 경우에는 B가 0의 reward를 받는 episode 한가지만 겪고 있다.
• MC와 TD를 돌렸을 때 V(A)와 V(B)는 어떻게 될까?

• MC 같은 경우에는 $G_t$의 에러, 즉 episode의 전체 trace의 에러를 줄이려는 방향으로 solution을 만든다.

  

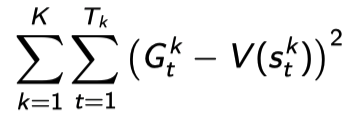
• TD 같은 경우에는 각 state의 에러를 줄이려는 방향으로 수렴하게 된다.

  • Maximum-liklihood Markov model)을 만드는 것과 마찬가지다. (state transition probability distribution과 reward probabilty를 모델링함)

    

    

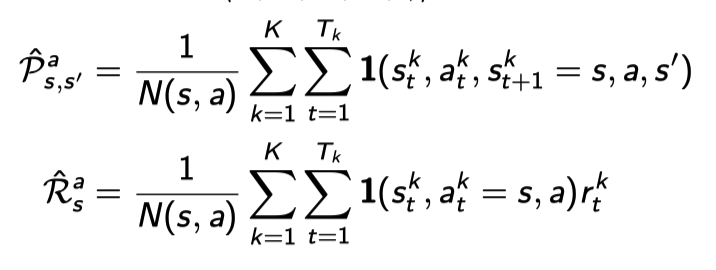
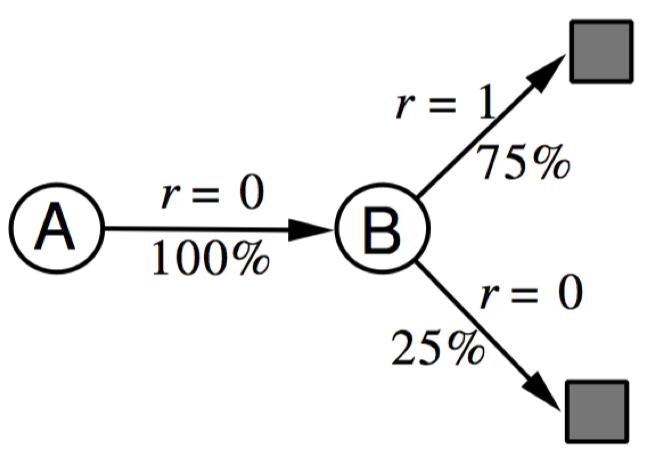
  • Markov property를 적극 이용하는 셈: V(A) ~ R(A)+$\gamma$V(B)

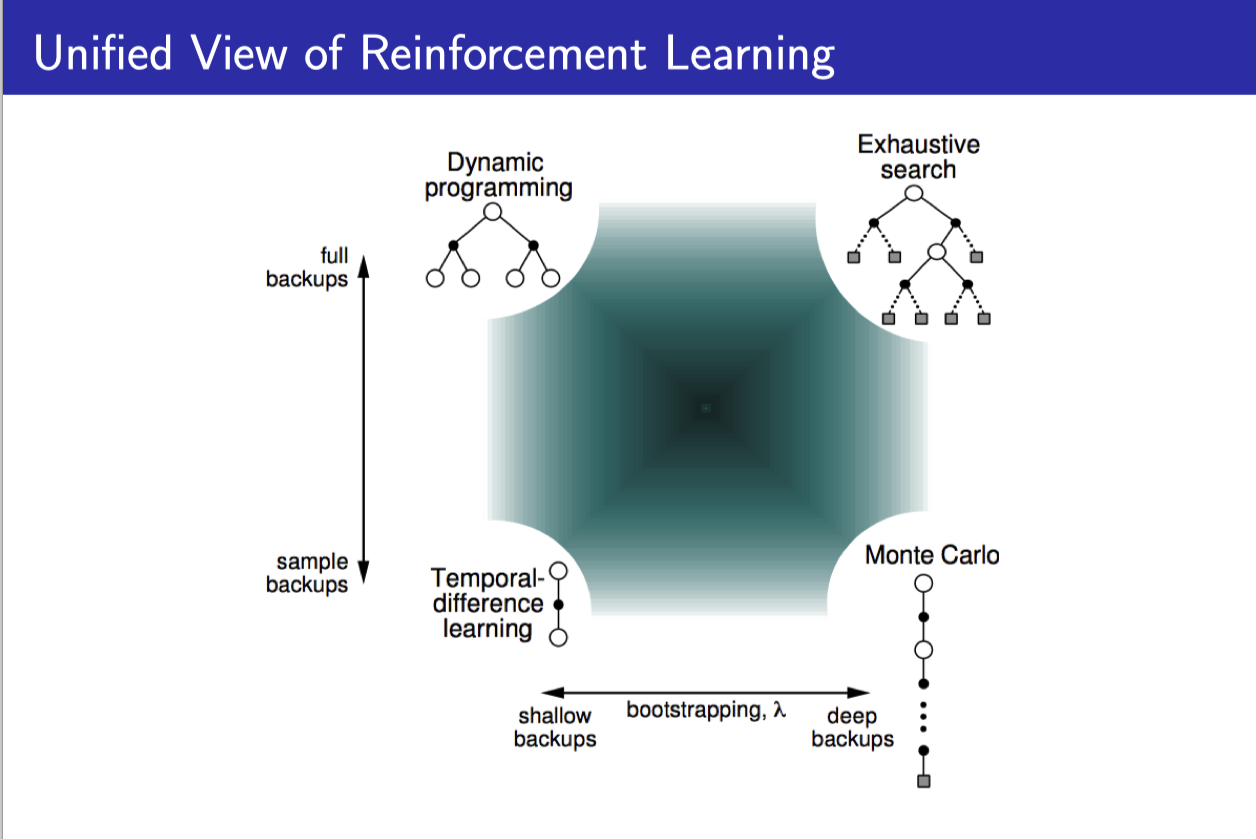
Dynamic programming, Monte-Carlo, and Temproal-Difference

policy evaluation process를 2가지 측면으로 나눠서 생각할 수 있다.

• Bootstrapping: estimate을 이용해서 state value를 update할 것인가
  • MC: 끝까지 episode를 진행한 후에 계산이 되므로 estimate를 쓰지 않음 ⇒ No bootstrapping
  • DP, TD: 다음 번 state value esimtation을 가지고 현재 state value를 update를 한다. ⇒ Bootstrapping
• Sampling: 나올 수 있는 경우의 수를 전부다 쓸 것인가 그 중 하나만 sample해서 쓸 것인가
  • MC, TD: 나올 수 있는 모든 state transition을 고려하는 것이 아니라 episode에서 실제 발생한 것만 sample해서 쓰는 것이므로 ⇒ Sampling
  • DP: 모든 state transition을 고려해서 update하므로 ⇒ No sampling

	Bootstrapping	No bootstrapping
No sampling	DP
Sampling	TD	MC

TD($\lambda$)

n-step prediction

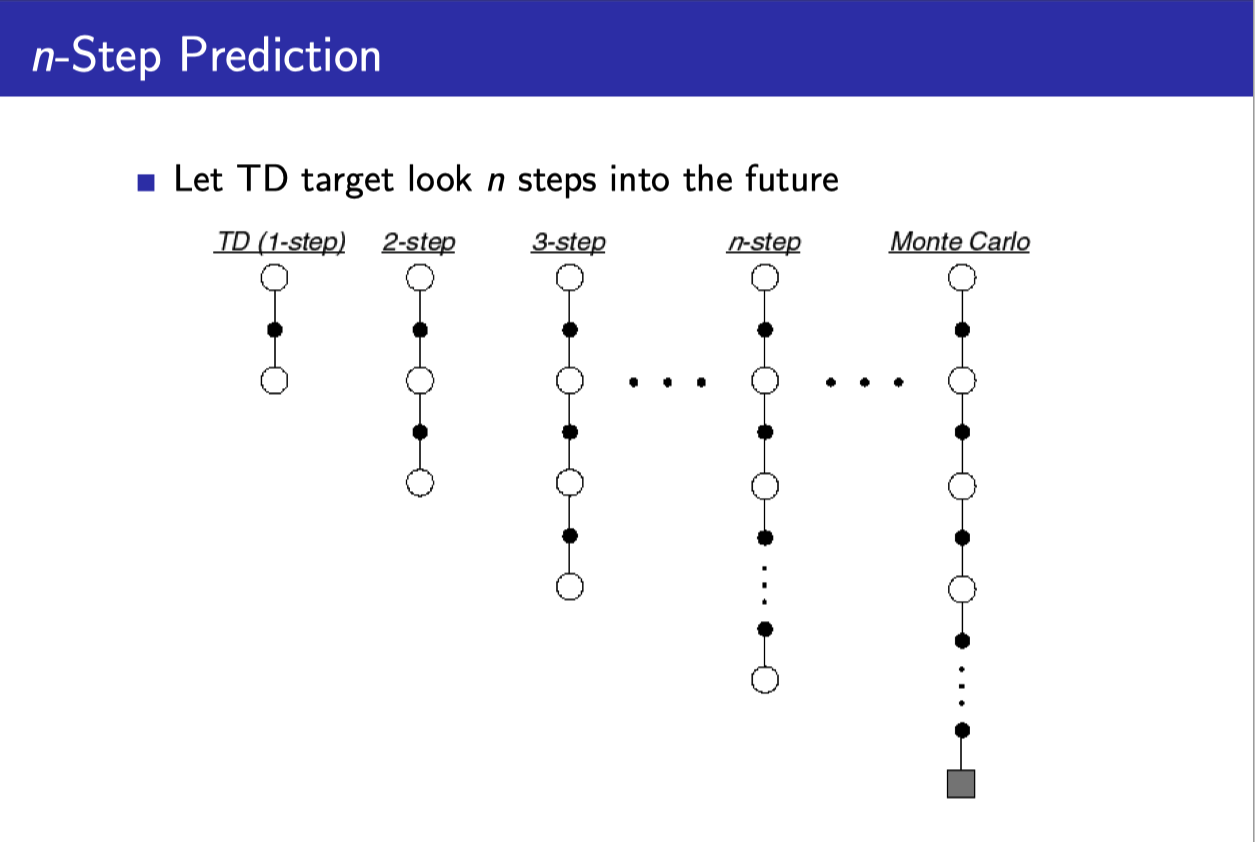
• 지금까지 봤던 TD의 경우에는 TD(0)로써 딱 현재의 step을 봤지만
• 여기에 변형을 주어서 n-step까지 활용하게 할 수도 있다.
• 이 n을 무한대로 늘려 놓은 것이 Monte-Carlo이다.

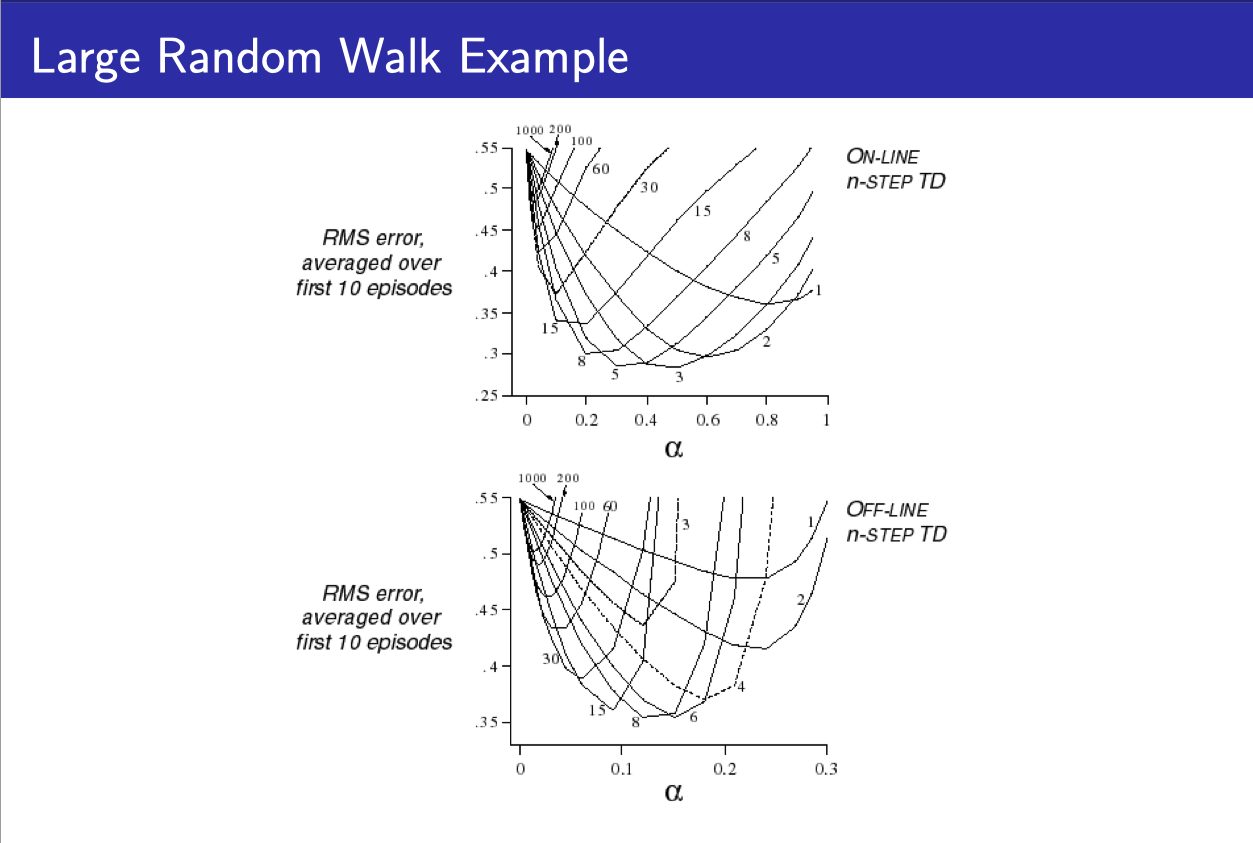
• 위의 그래프는 다양한 n-step을 이용했을 때의 RMS을 보여준다.
• 1이 TD이고, 숫자가 커질수록 MC가 된다.
• 주목할 점은 에러가 가장 작아지는 특정한 n이 존재한다는 점이다.

Averaging n-Step returns

• 그렇다면 우리는 어떤 n을 써야할까?
• 이러한 점을 확실히 모르기 때문에 우리는 여러가지 n을 함께 써서 평균을 내는 방법으로 optimal n을 모르더라도 적당히 좋은 결과를 얻을 수 있다.
• 위의 에제에서는 n=2와 n=4를 함께 이용하였다.
• 그렇다면 몇 개의 n을 섞을 것이며 어떤 n들을 섞을 것인지 어떻게 정할 것인가?

TD($\lambda$)

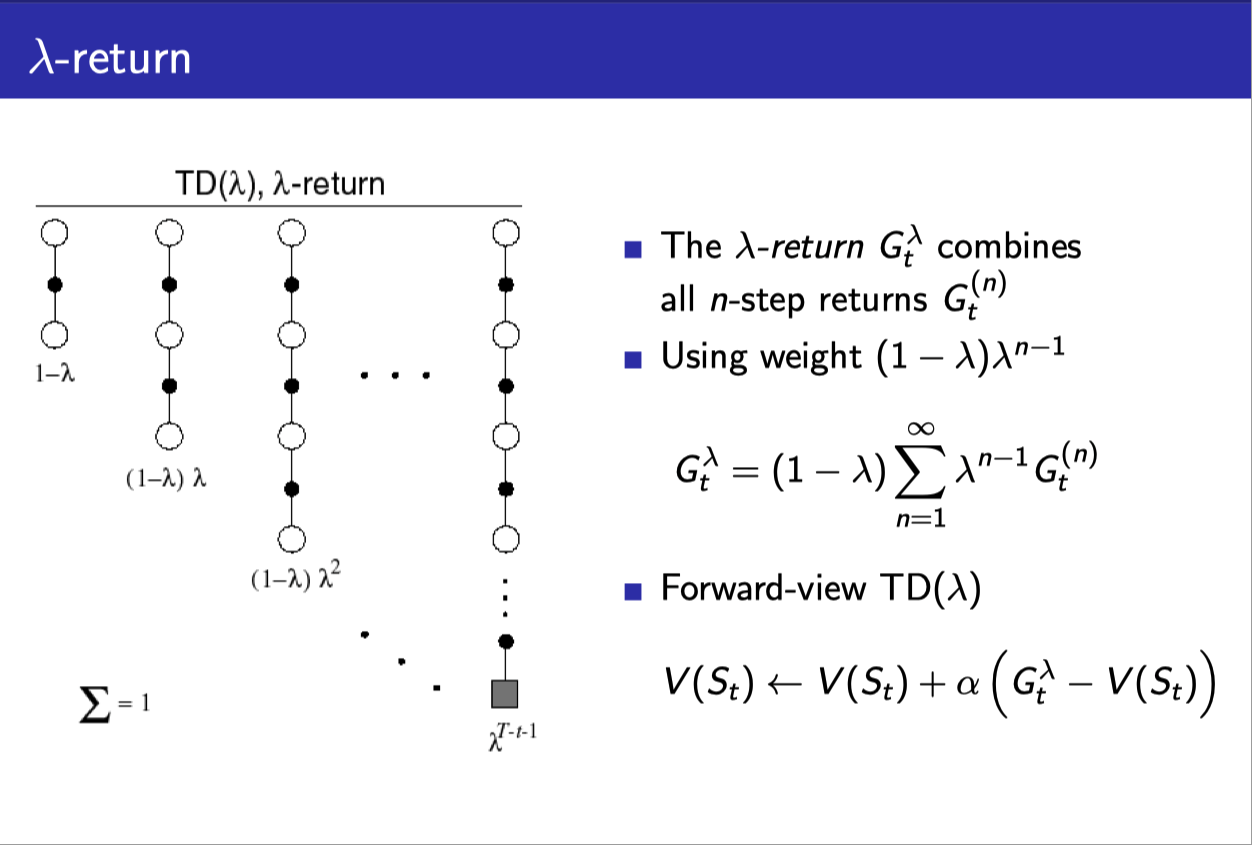
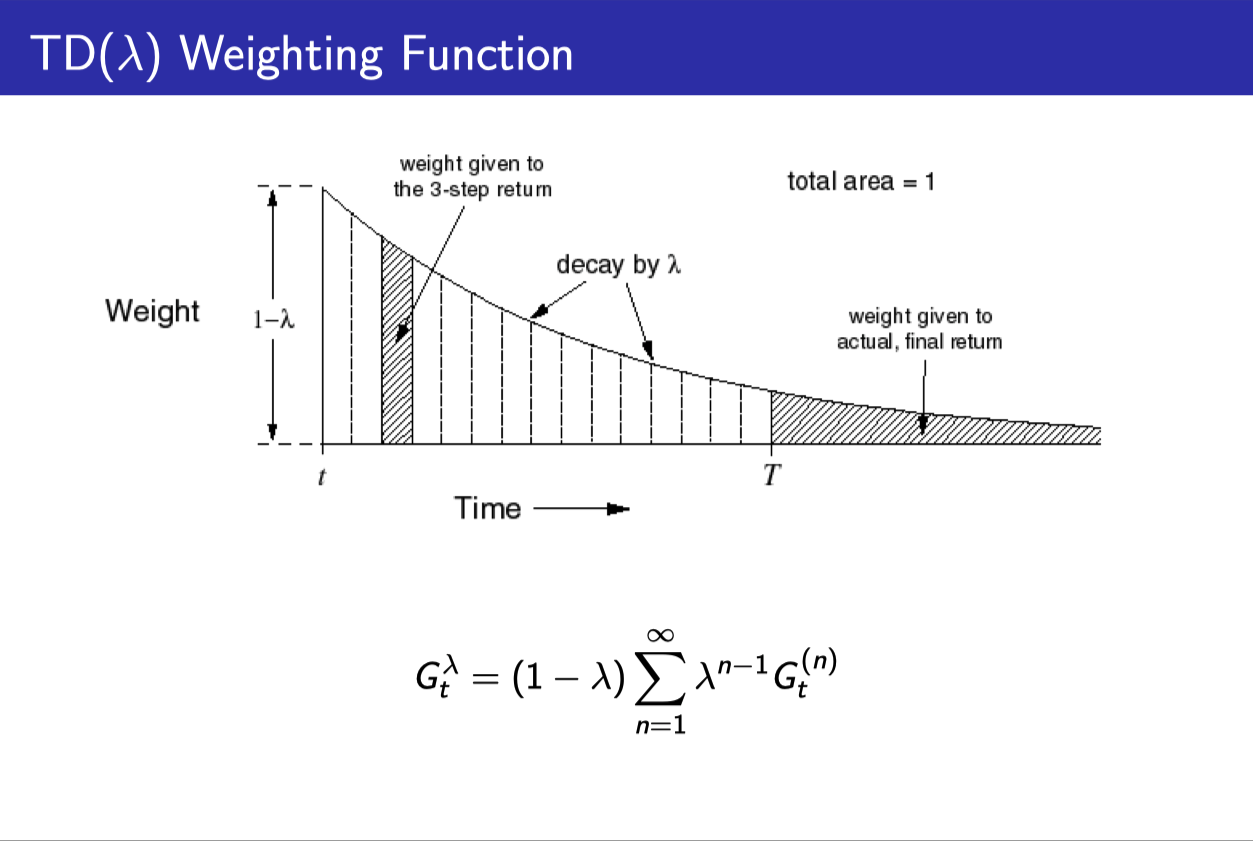
• $(1-\lambda), (1-\lambda)\lambda, (1-\lambda)\lambda^2, \cdots$처럼 weight를 만들어서
• 각각의 Return estimate($G_t^{(n)}$)에 곱해준다.
• 그러면 몇개의 n-step을 섞어 넣던 weight들의 합이 1이 되게 된다.
• (당연히 1-step return이 가장 큰 비중을 차지하게 될 것이다.)

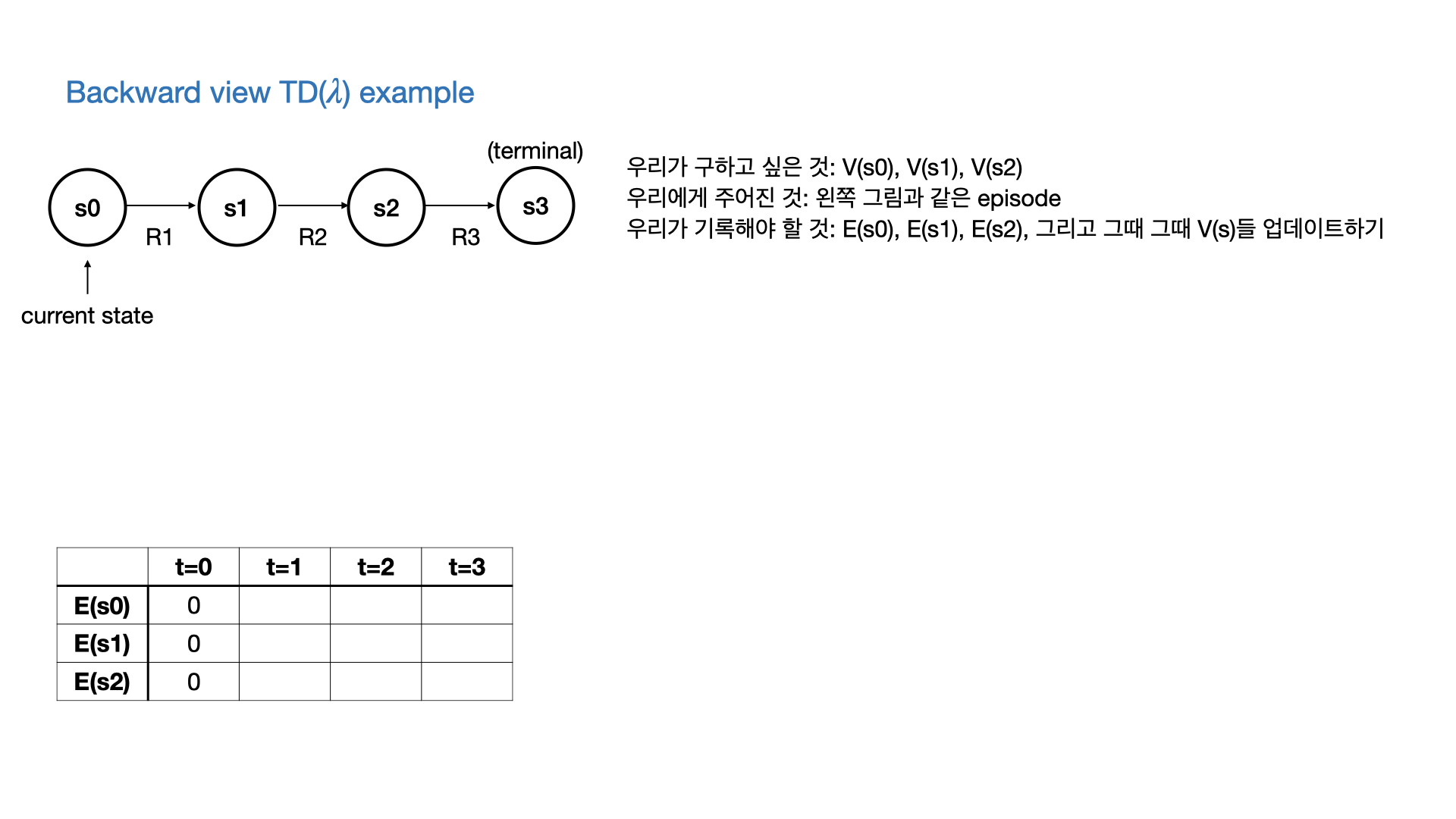
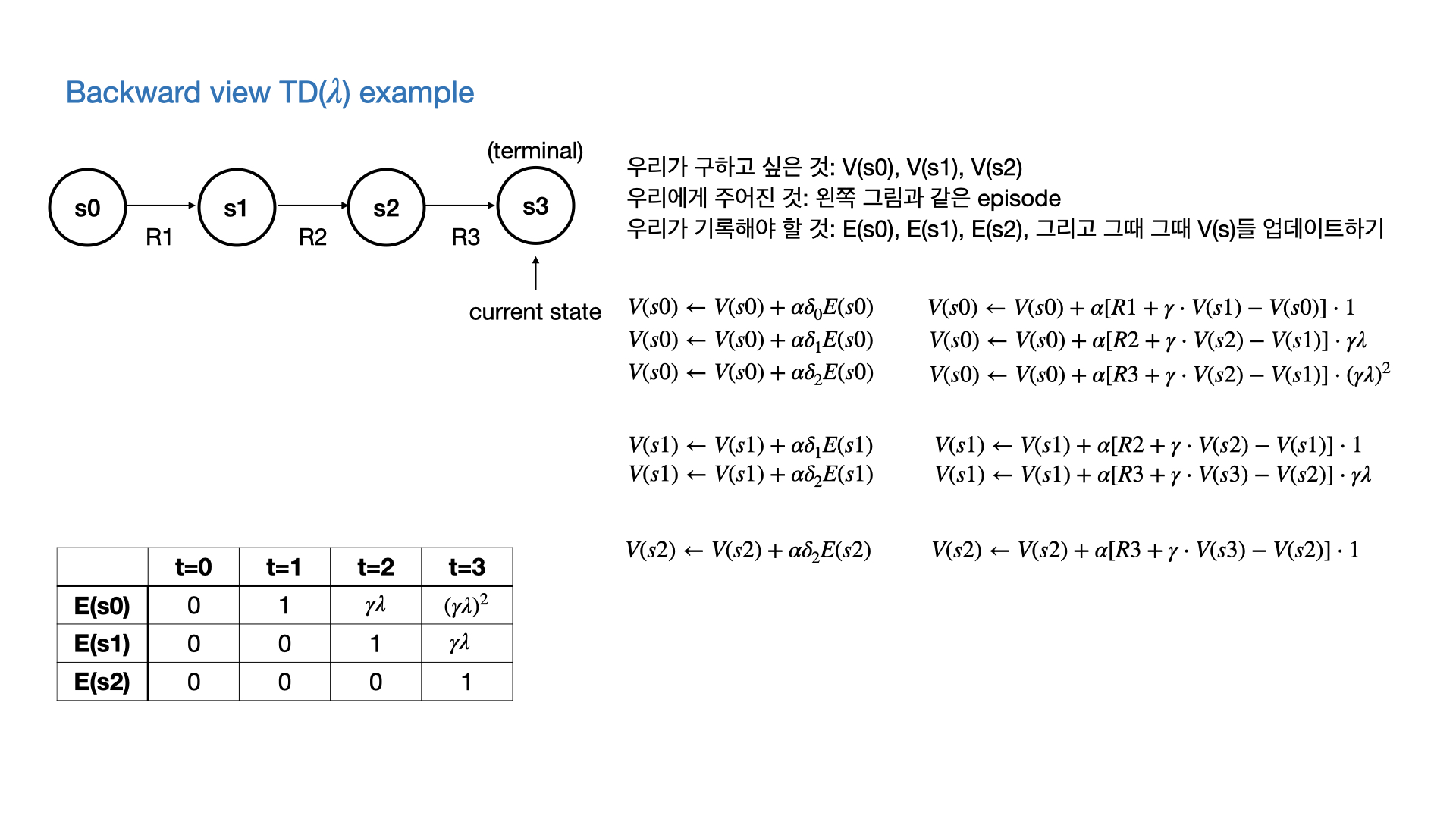
Forward view and backward view of TD($\lambda$)

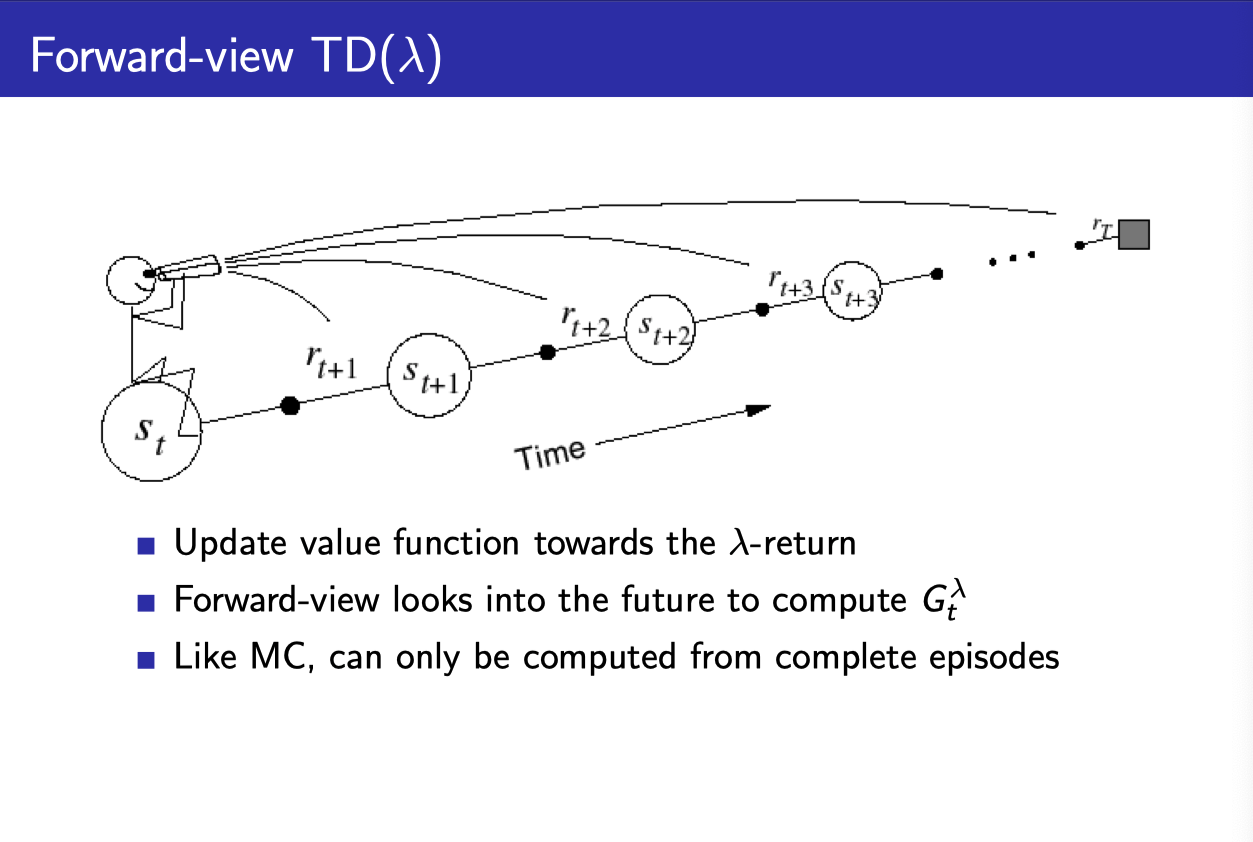
• 결국 MC와 마찬가지로 TD($\lambda$)를 계산하기 위해서는 다음 state들과 그에 해당하는 return들이 필요하다.
• 따라서 episode가 끝나야지만 계산할 수 있다. (이론적으로는 그렇다.)

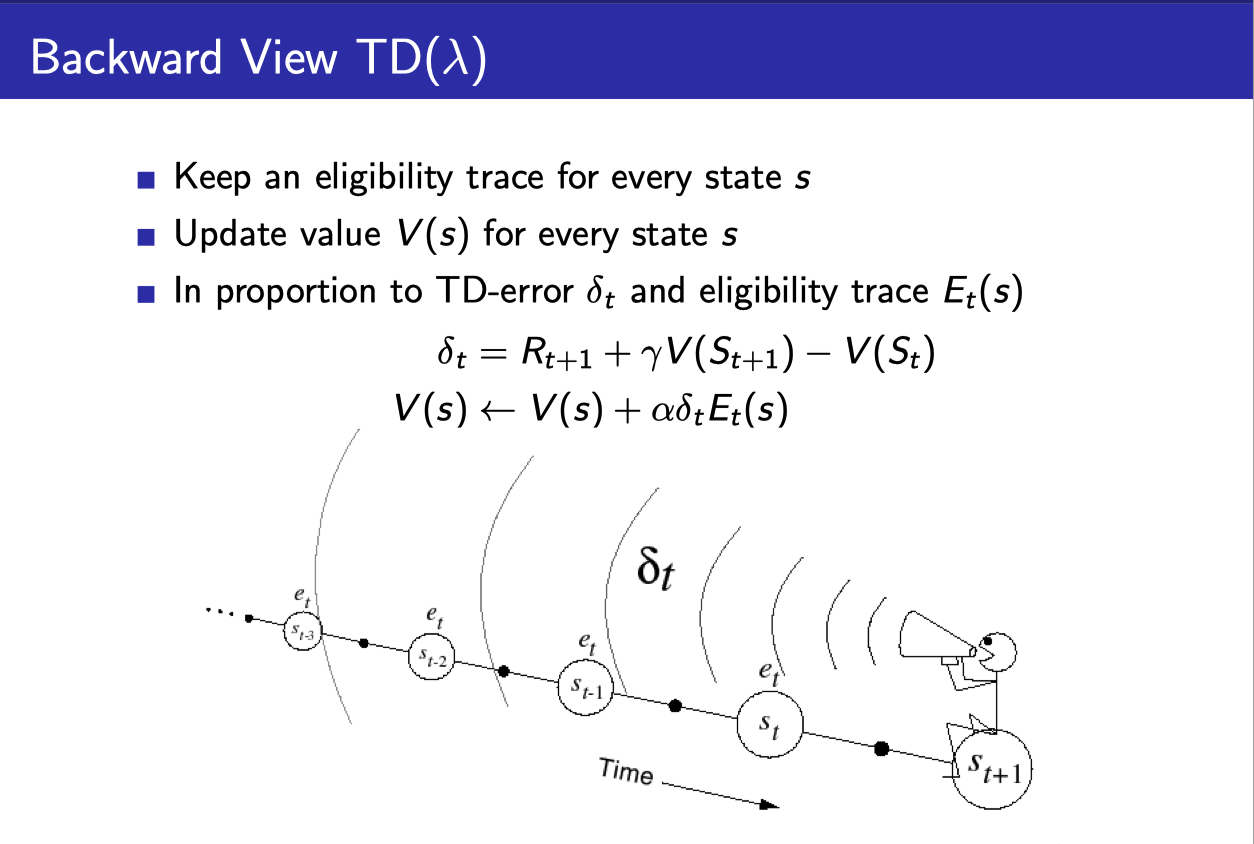
• 하지만 실제로 TD($\lambda$)를 구현할 때는
• Eligibility Trace라는 것을 각 state마다 기록해서
• 필요한 정보가 나온 곳까지의 $G_t^{(\lambda)}$까지 기록해준다.

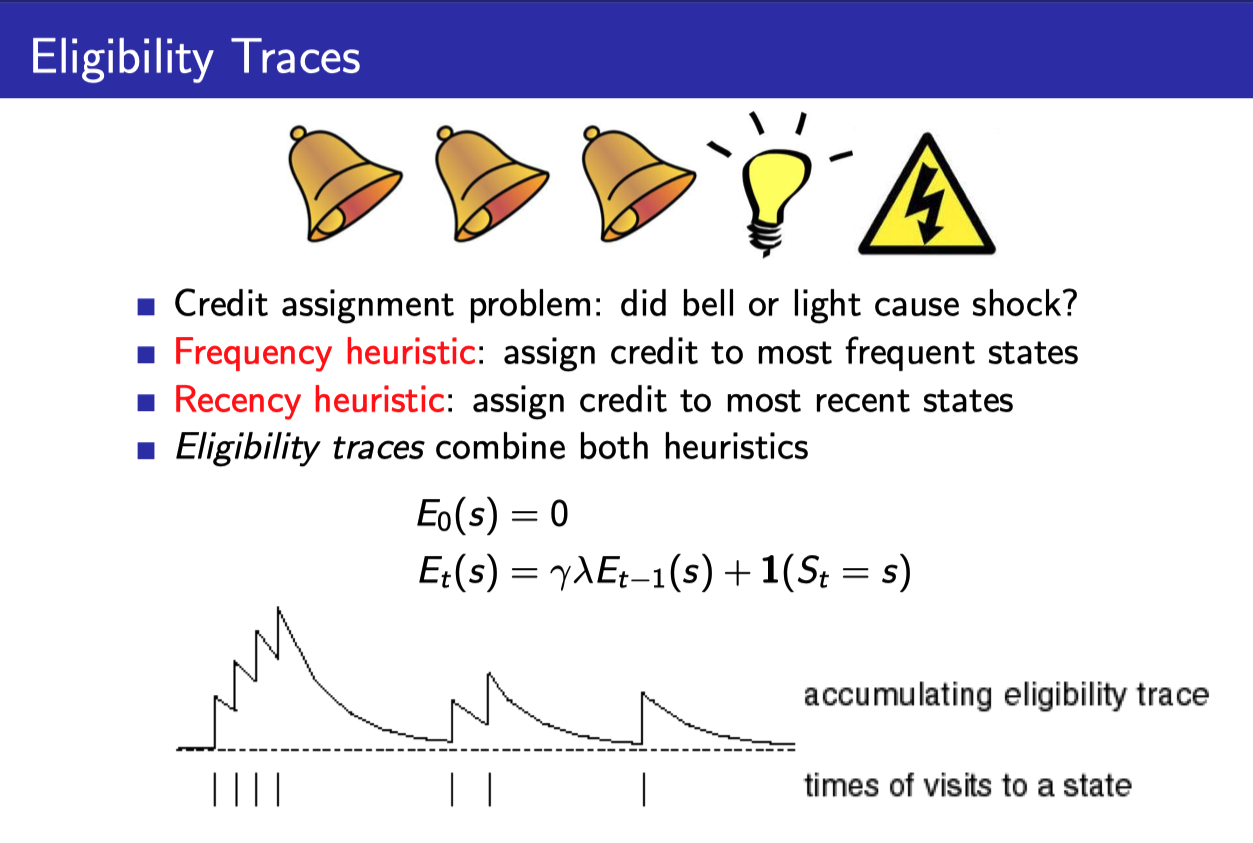
• Eligibility trace라는 것은 위와 같이 계산할 수 있다.
• $\gamma$에 의해서 episode가 진행됨에 따라 값이 서서히 줄어든다. (최근의 state visit에 더 가중치를 주는 Recency heuristic)
• 그리고 state visit마다 1씩 더해준다. (얼마나 자주 visit하는지에 가중치를 주는 Frequency heuristic)

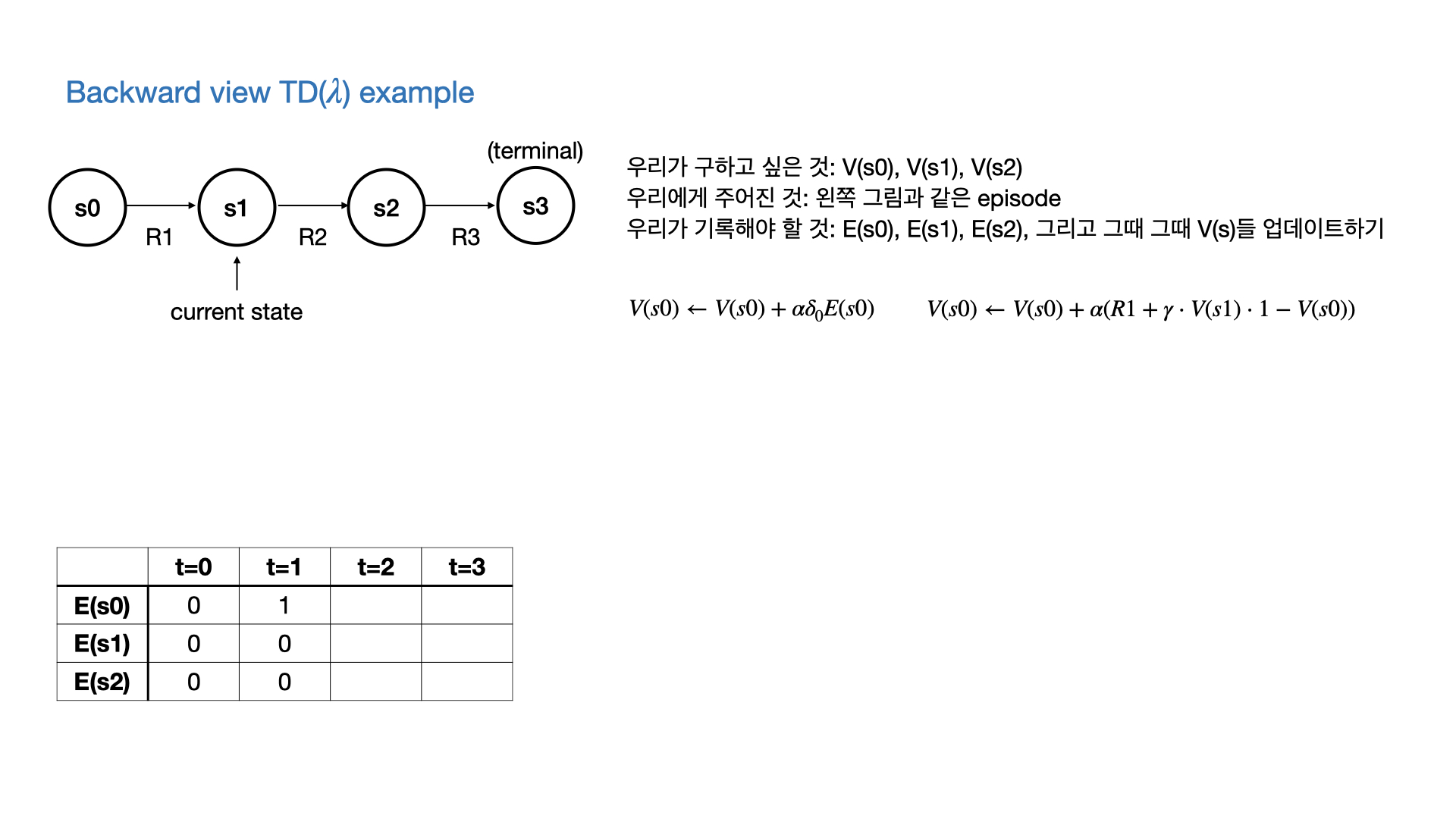
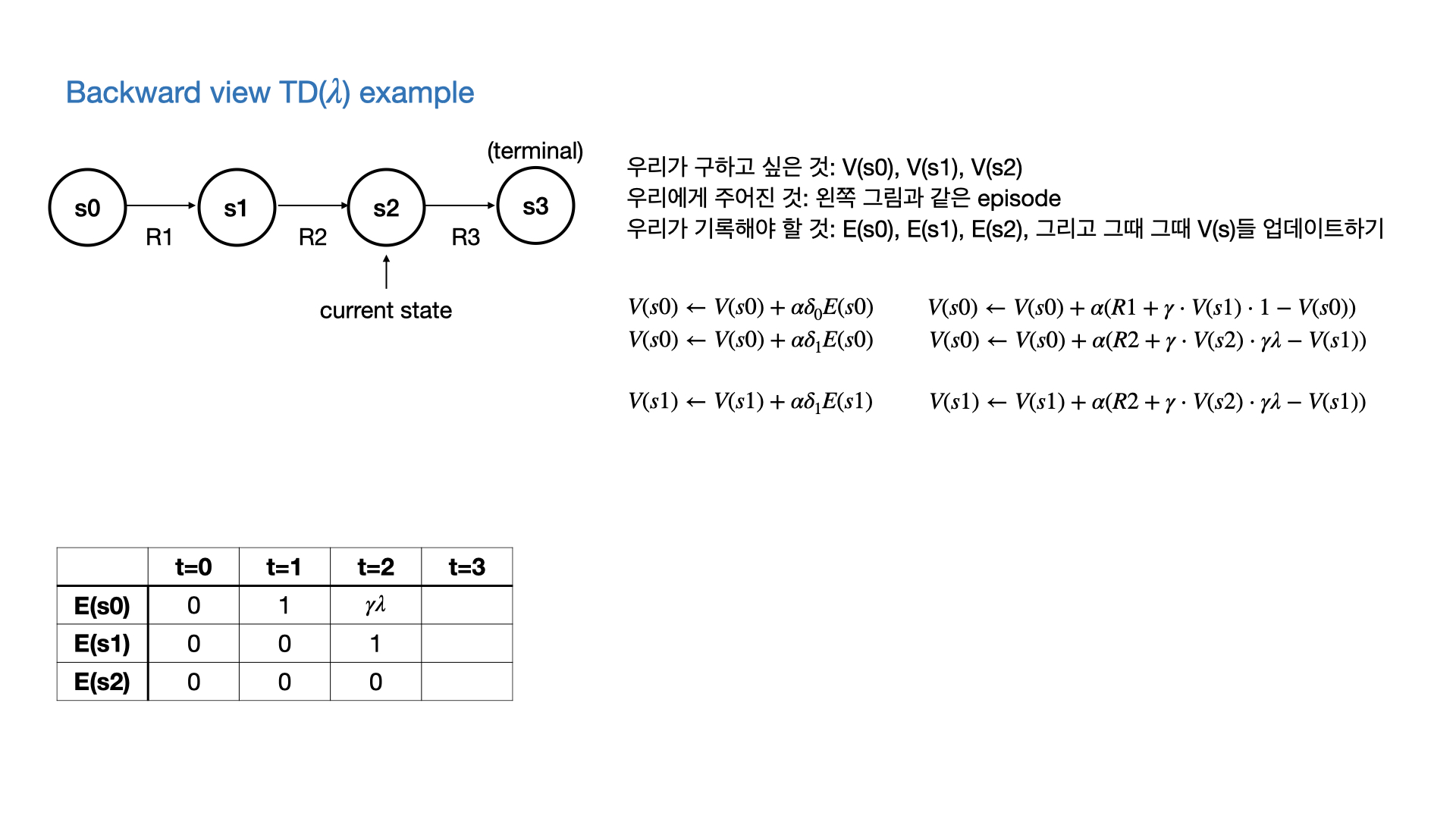
$\lambda$에 따른 backward view와 forward view와의 관계

• 당연히 forward view는 모든 episode가 끝나야 완성이 되고, backward view와 같아지므로 onlie update일 경우에는 forward view ≠ backward view인 순간들이 있다.
  • 위에서 쓴 Eligibility trace말고 변형을 사용하면 online일 때도 같다고 한다.
• 그러나 기본적으로 backward와 forward는 같아야 하고, $\lambda=0$일 때는 TD(0), $\lambda=1$일 때는 every visit MC와 equivalent하다.