[Study] Markov Decision Process

본 글은 David Silver의 강의를 듣고서 정리한 글이다. 매우 오래 전에 공부한 마코프 이론을 다시 한 번 상기시키기 위해 기초 강의와 함께 꼼꼼히 정리하면서 상기시켰다.

1. Markov Processes

1.1 Introduction to MDPs

• Markov decision processes : 강화학습에서 Environment 를 묘사하는 방법
• 이 때, MDP 로 묘사하는 경우, environment 는 관측이 가능한 environment 인 상태입니다. (fully observable)
• 대부분의 RL problem은 MDP 로 표현이 가능합니다.
  • Optimal control → continuous MDPs
  • Partially observalble problems → MDPs
  • Bandits → MDPs with one state
  • 즉, 모든 RL problem의 기본원리를 이해한다면, MDP로 표현할 수 있다는 것을 확인할 수 있습니다.

1.2 Markov Property

• The future is independent of the past given the present = 미래는 현재에만 종속적이며, 그 이전의 과거와는 독립적입니다.

$$
P[S_{t+1}|S_t] = P[S_{t+1}|S1, …, S_{t}]
$$

1.3 State Transition Matrix

• current state $s$, successor state $s’$, the state transition probability $P_{ss’}$
  • $P_{ss’}$는 현재 s state 에서 $s_{t+1}=s’$ 으로 변이 되는 조건부 확률

$$
P_{ss’}=P[S_{t+1}=s’|S_{t}=s]
$$

• State transition matrix $P$ : 위의 transition probability 를 모든 s → s’ 에 대해 모아 놓은 행렬
  • transition probability matrix

$$
P = \begin{matrix}P_{11}…P_{1n}\.\.\.\P_{n1}…P_{nn}\end{matrix}
$$

$P_{1n}$ : 현재 state 1에서 → Next state n로 전이되는 확률

따라서, 각 행(row)의 합은 1이다. P11 + … + P1n = 1, state 1에서 다른 state 로 뻗어나가는 확률은 한번에 한 경우의 수밖에 없으므로 모든 경우의 확률의 합은 1입니다.

1.4 Markov Process

• Markov process 는 memoryless random process
• Markov Process (or Markov Chain) 는 <S, P> 로 표현합니다.
  • S 는 유한한 state 들의 집합입니다. (finite set of states)
  • P 는 transition probability matrix

1.5 Example of Markov Chain

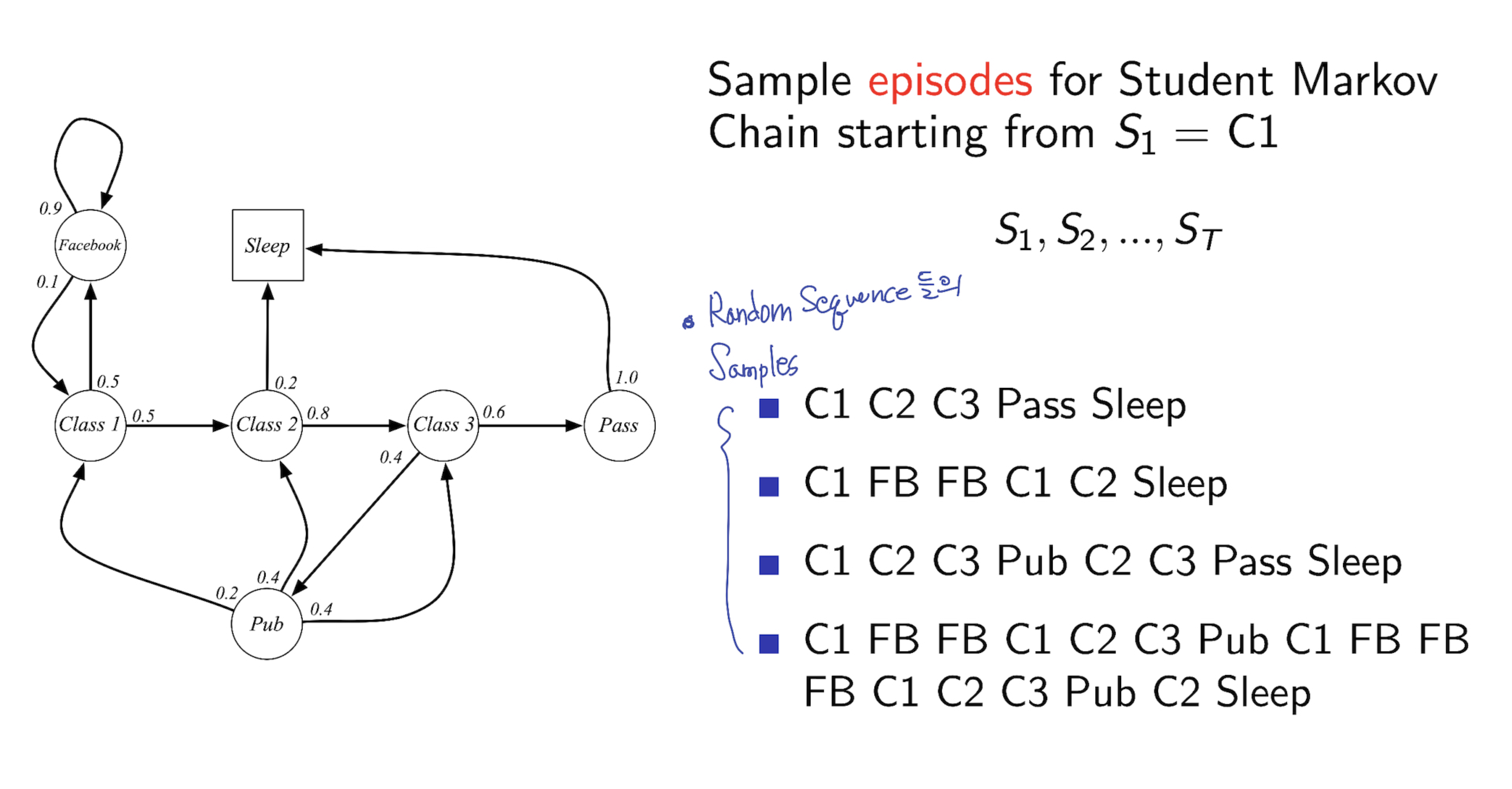
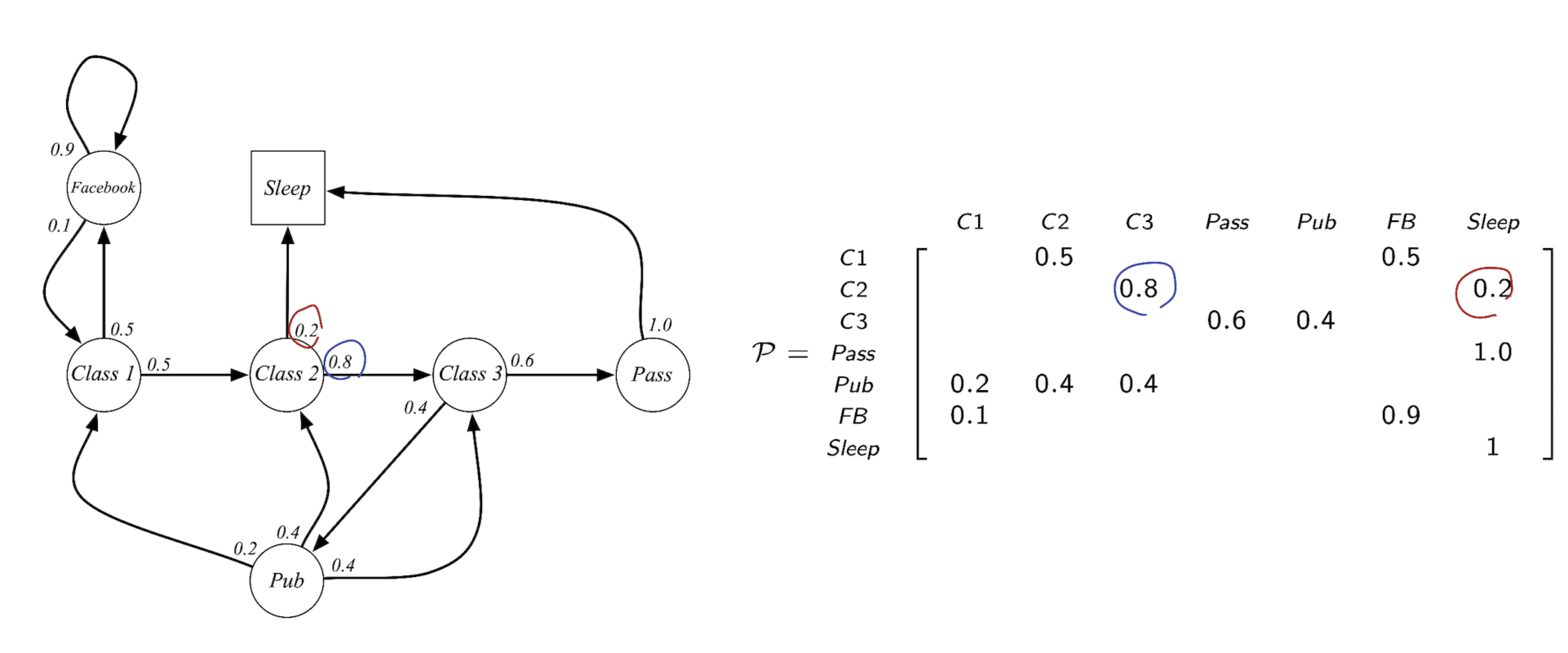
아래 그림에서 처럼, Class 2 State 에서 다음 state 로 넘어갈 확률 0.2, 0.8 을 오른쪽 transition probability matrix 에서 확인 할 수 있습니다. state 2 → state 3 으로 가는 확률 0.8, state 2 → state sleep 0.2 를 확인 할 수 있습니다.

2. Markov Reward Processes

2.1 MRP: Markov Reward Process

• MRP란? Markov chain 에 VALUE 가 더해진 chain

Expression: Markov Reward Process → <S, P, R, $\gamma$>

• S : states set

• P: transition probability matrix

  $P_{ss’}=P[S_{t+1}=s’|S_{t}=s]$

• R: reward function , $R_{s}=E[R_{t+1}|S_{t}=s]$

• $\gamma$: discount factor, 0≤$\gamma$≤1

2.2 Return

$$
G_{t }=R_{t+1}+\gamma R_{t+2} + … = \Sigma_{k=0}^{inf} \gamma ^k R_{t+k+1}
$$

• return Gt는 현재 t 에서부터, 모든 discount 된 reward 의 합입니다.

• return 과 reward 헷갈리지 말아야합니다! return 은 지금부터 미래까지 합 (단, discount 그 의미는 수학적 계산편의도 있지만, 미래에 가중치를 얼마나 두느냐의 문제도 있습니다), reward 는 현재 state 와 action 이 환경으로 받은 값

• 왜 DISCOUNT 하는가?

2.3 Value Function

• Value Function : $v(s)$ -“ total reward we will get. This is the value we care about “
  • RL 에서 우리가 신경써야하는 최종 형태의 total reward function

$$
v(s)=E[G_{t}|S_{t}=s]
$$

• Example:

2.4 Bellman Equation for MRPs

• Value Function 은 다음과 같이 쪼개 질 수 있다.
  • immediate reward $R_{t+1}$
  • discounted value of successor state $\gamma v(S_{t+1})$
  • 지금 현재 state 에서의 reward(immediate reward) + 미래의 value(value where agent end up)
• $v(s) = R_{t+1}+\gamma v(S_{t+1})$

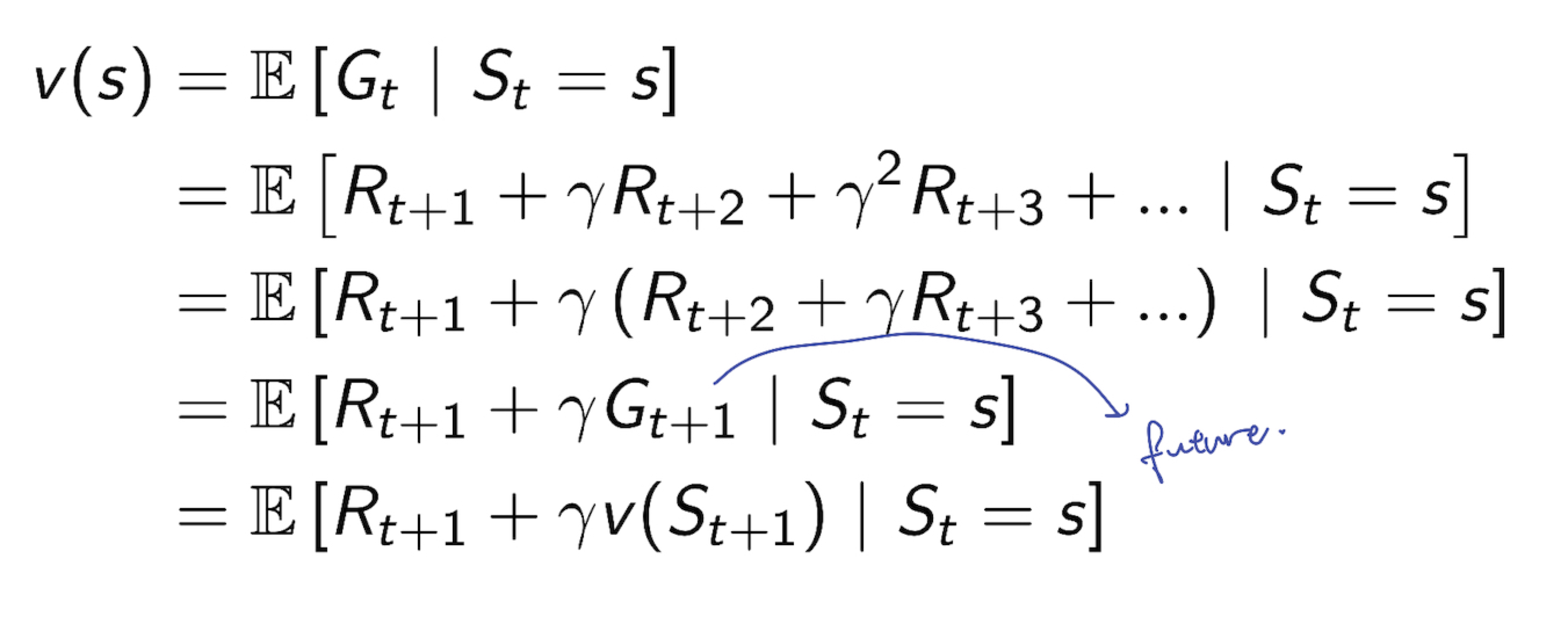
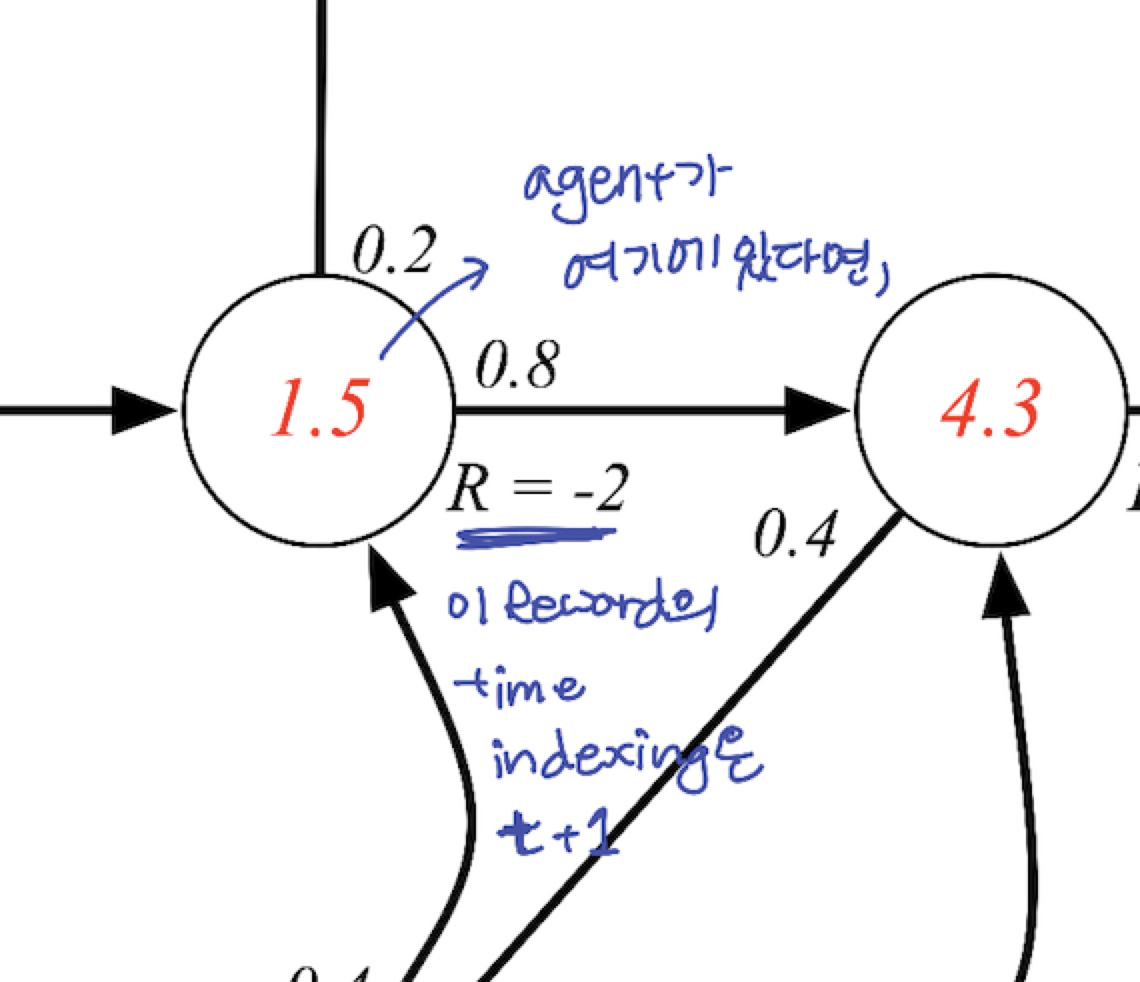
• Q) 왜 R index 가 t+1 인가? : agent 와 environment 사이에서의 경계문제. agent 가 environment 에서 활동하는 순간 time stamp 가 지나게 됨. agent 의 액션이후 environment 로부터 영향을 받고 나오면 time stamp 가 그 다음으로 찍히는걸로 정의하기에, R t+1 이라 indexing 하게됨. 추후 강의에서 더 자세히 설명. just convention

2.5 Bellman Equation in Matrix Form

• 위 식을 Matrix 형태로 표현 한 것입니다.
• 아래의 식은 각각 Vector 라고 생각합니다

$$
v = R +\gamma Pv
$$

, where v = [v(1) … v(n)], R = [R1 … Rn] , P = [P11 .. P1n … P11 Pnn] (matrix)

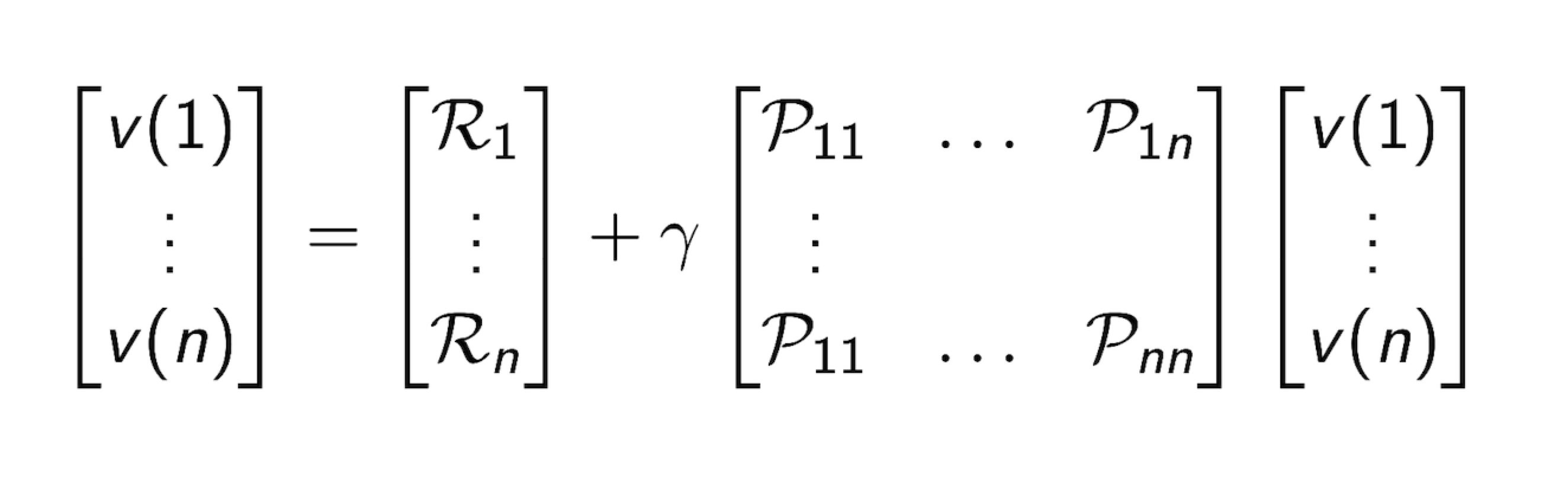
• Bellman Equation 을 풀기 위해서는, 실제 작은 사이즈에서는 linear equation 을 풀기 쉽지만, 큰 규모의 문제에서 실제로는 iterative methods 를 사용한다.
  • Dynamic programming
  • Monte-Carlo evaluation
  • Temporal-Difference learning

2.6 Solving the Bellman Equation

• 식 자체를 푸는 것은 어렵지 않다. linear equation. 손으로 풀기엔.. 그리고 연산장치를 이용한 연산 역시 작은 사이즈에선 문제되지 않는다. 다만, 사이즈가 크면 클수록 가장 마지막 식의 역행렬을 구할때 연산량이 많이 필요하다. 따라서 다른 방법이 필요하다.

$$
v=R+\gamma Pv \ (I-\gamma P)v = R \ v = (I-\gamma P)^{-1}R
$$

• Computation을 위해선 세가지 iterative한 방법을 사용한다
  • Dynamic Programming
  • Monte-Carlo Evaluation
  • Temporal-Difference Learning
  • 위 세가지의 자세한 내용은 추후에 등장 예정

3. Markov Decision Processes

• MDP가 실제로 우리가 RL 에서 자주 사용될 개념 “Actually Use in RL”
• MDP Expression: Markov Decision Process → <S, A, P, R, $\gamma$>

3.1 Policy

• Policy 정의: Policy $\pi$는 주어진 현재 state 에서 Action 에 대한 분포이다.(한국말이 더 어렵기에, distribution over actions given states)

$$
\pi (a|s) = P[A_{t}=a | S_{t}=s]
$$

• Policy 는 agent 의 행동을 결정한다.
• Policy 는 현재 state (current state)에 영향을 받는다(depend on current state, not history)
• Policy 는 Stationary 라 가정한다.(time-independent)

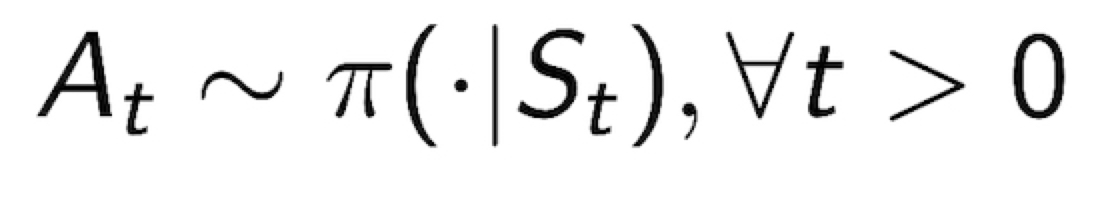
• MDP M = <S, A, P, R, $\gamma$ >, Policy = $\pi$ 일 때,

  • State sequnce S1, S2, S3 … : <S, $P^{\pi}$> 는 Markov Process

  • State and Reward Sequence S1, R2, S2, R2 … : <S, $P^{\pi}, R^{\pi}, \gamma$>는 Markov Reward Process

  • where P와 R은 다음과 같다

    

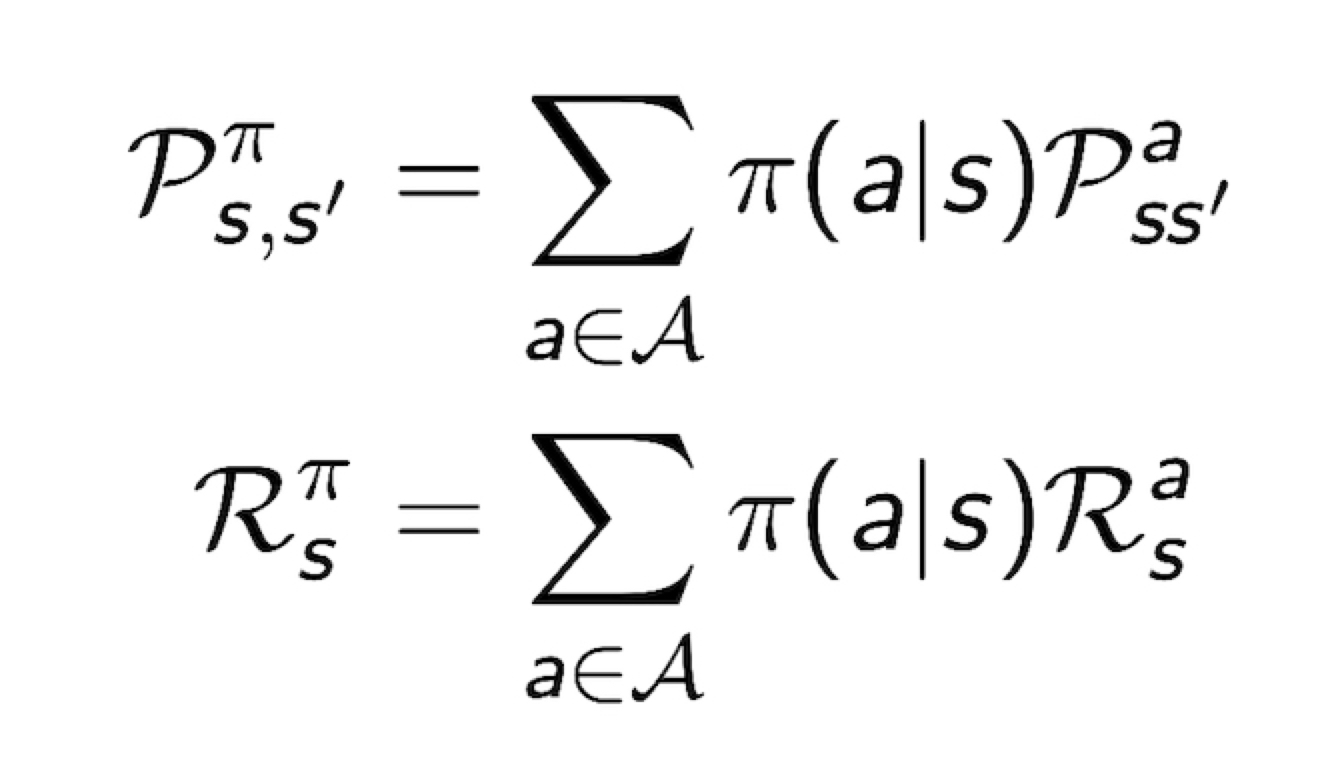
3.2 Value Function

• Value function 과 Action-Value function
  • value fuction: how good in policy with state s
  • action-value function: how good in policy with state s, action a

3.3 Bellman Expectation Equation

이 뒷 내용부터는 실질적으로 Equation 과 State Diagram 등이 피부에 와닿지는 않는다. 실제로 강의가 진행되면서 application 이나 본 내용이 담긴 problem을 직접 만나보고, 각 경우가 이것을 의미했던 것이구나 하며 feedback 이 있어야 더욱 잘 이해될 내용들이라고 생각된다

3.4 Bellman Expectation Equation for $V^{\pi}$

• 이 지점에서 Policy 역시 Distribution 혹은 Process(Sequence)의 형태로 개념을 확장해 간다. 다만 위의 value function 에 대한 정의에서 크게 벗어나지 않으며, 전체 state과 action 에 dependent 하다.

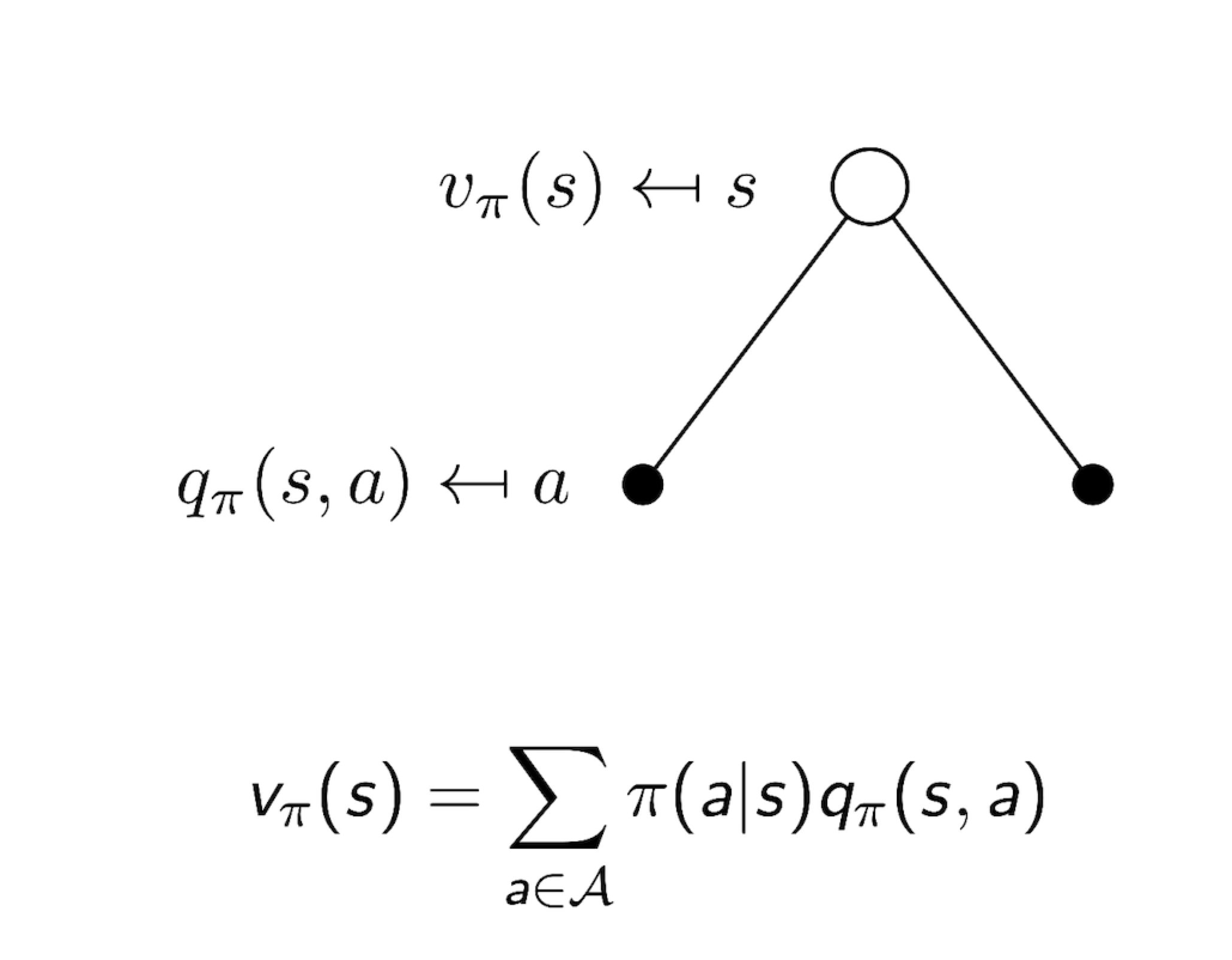
3.5 Bellman Expectation Equation for $Q^{\pi}$

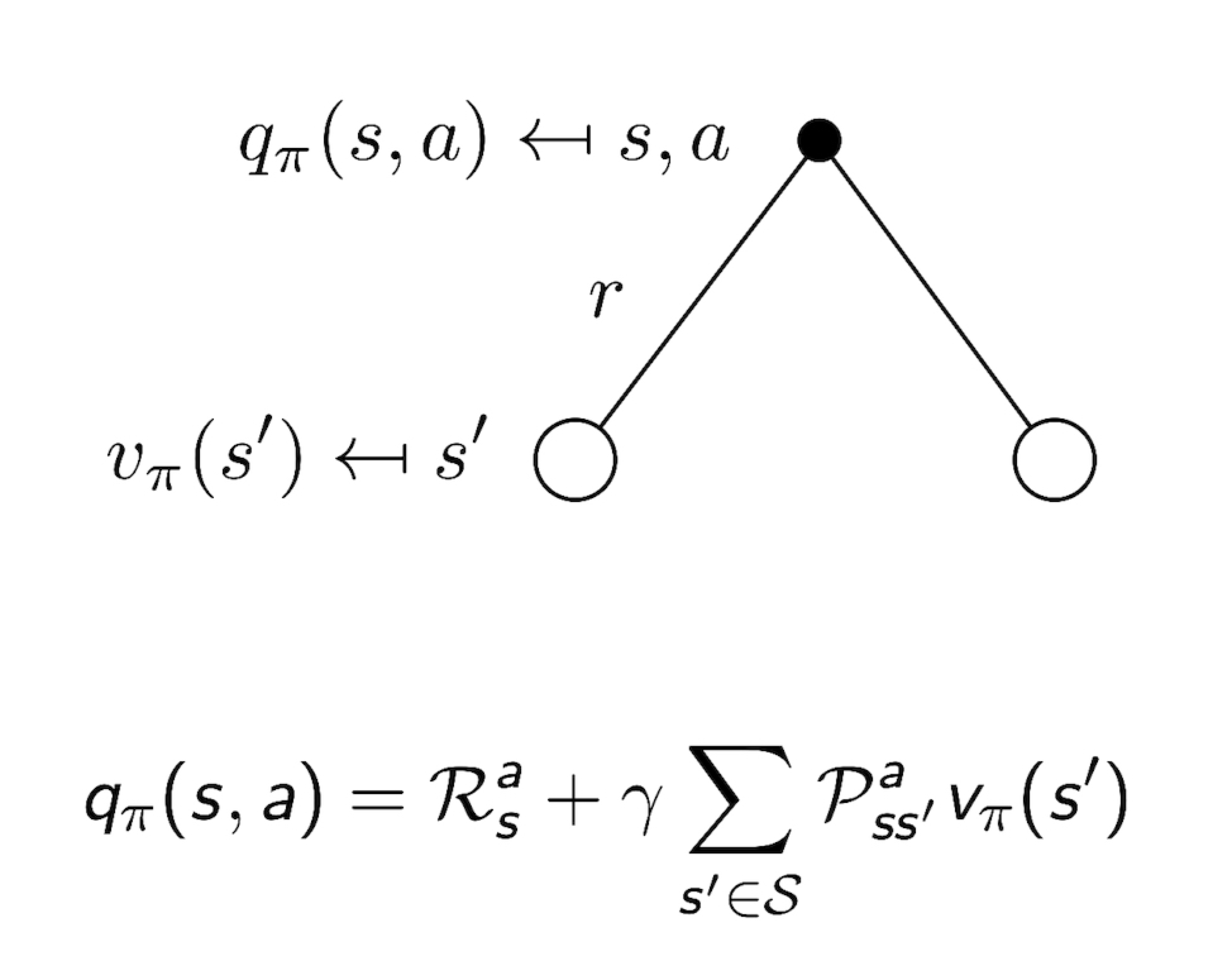
3.6 Bellman Expectation Equation for $v_{\pi}$

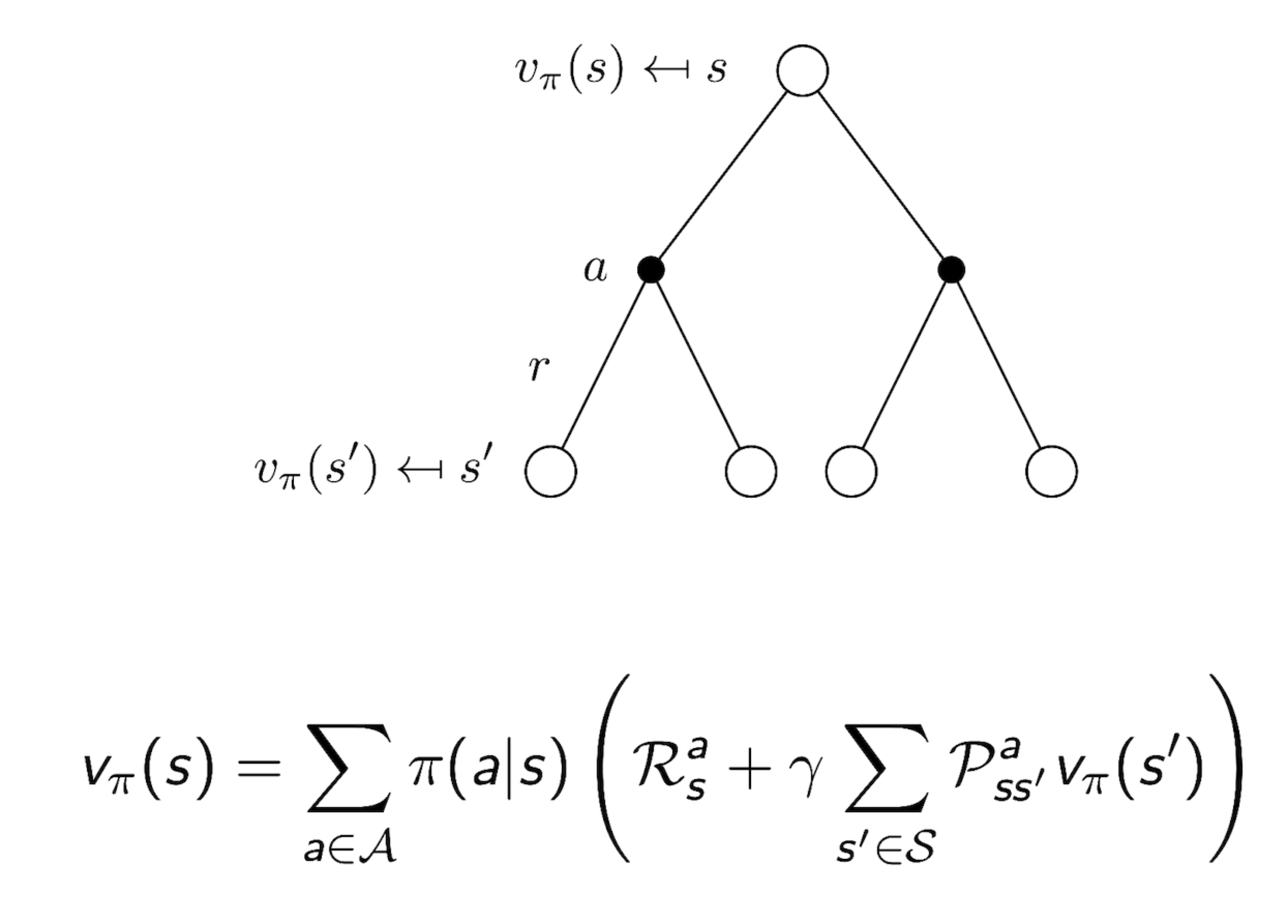
3.7 Bellman Expectation Equation for $q_{\pi}$

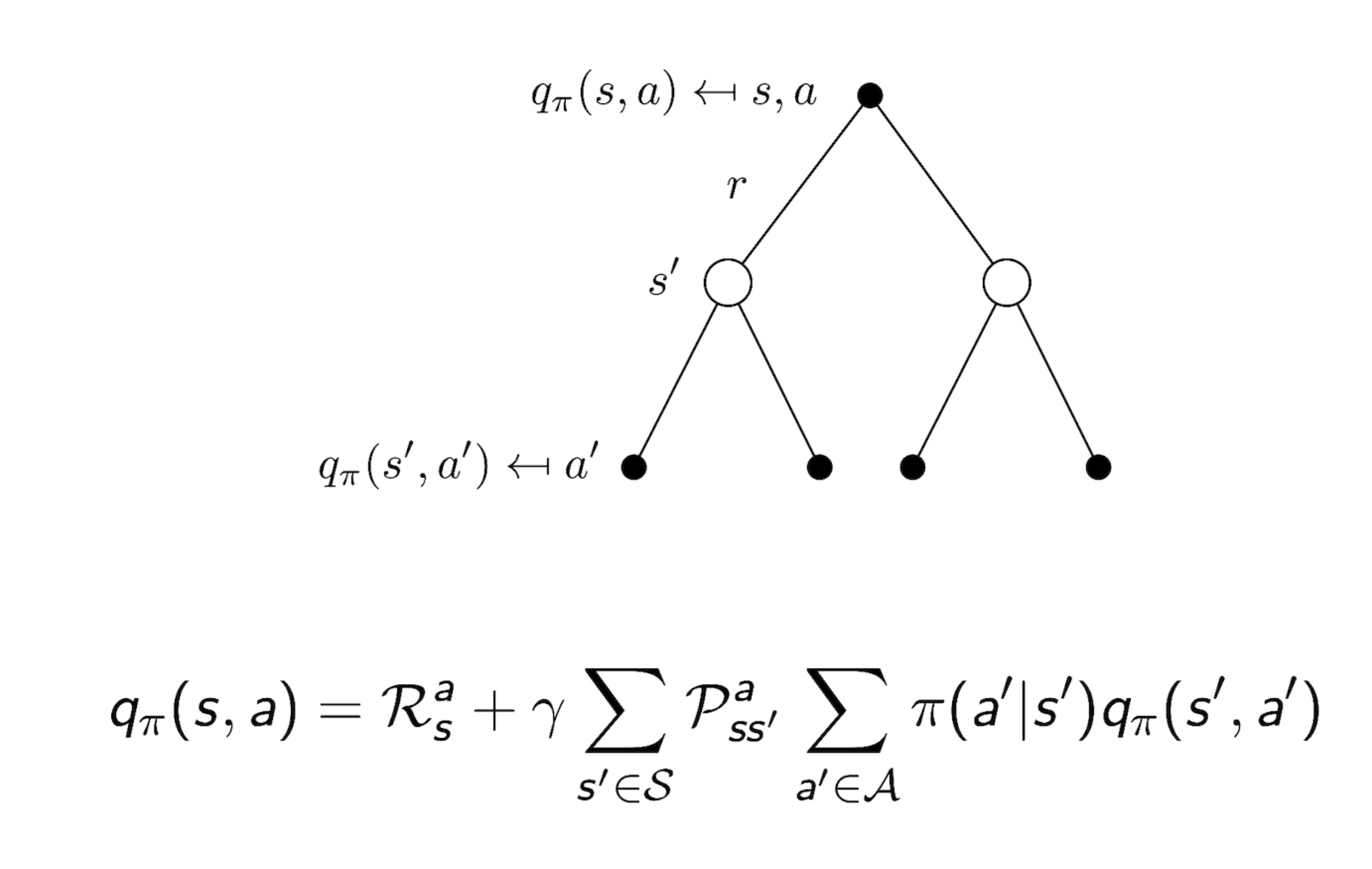
3.8 Bellman Expectation Equation (Matrix Form)

• Bellman expectation equation 역시, 다음과 같이 표현될 수 있고, 이에 관한 풀이법 역시 linear equation 이다.

$$
v_{\pi}=R^{\pi} + \gamma P^{\pi}v_{\pi}
$$

$$
v_{\pi}=(I-\gamma P^{\pi})^{-1}R^{\pi}
$$

3.9 Optimal Value Function

• optimal state-value function 은 모든 policy 에 대해서 maximum value function 을 찾는 문제이다

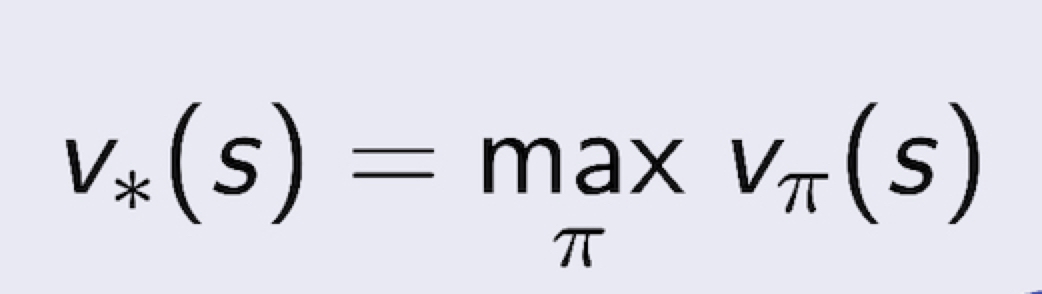
• optimal action-value function 역시 모든 policy 에 대해서 maximum action-value function 을 찾는 문제이다.

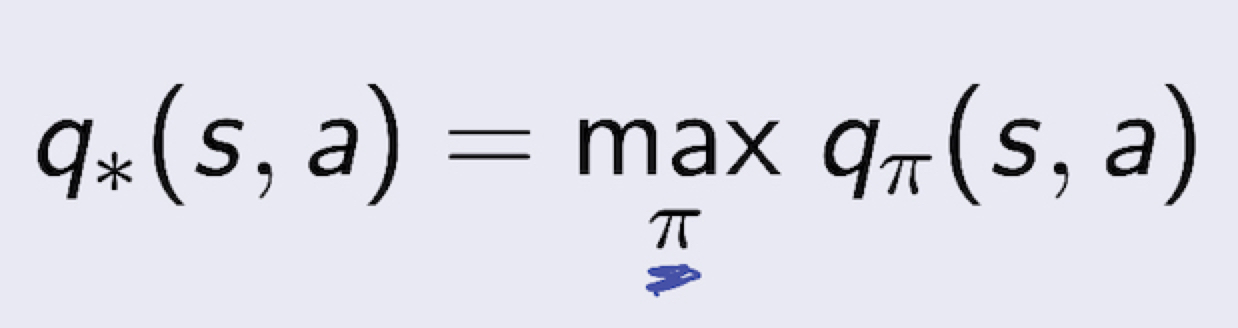
• Optimal value function 은 MDP에서 best possible performance 를 찾는 문제라고 볼수 있다.
• 즉, MDP is “SOLVED” when we know the optimal value function (q*, v*)

3.9 Optimal Policy

• Optimal Policy 문제는, Best Action to MDP 를 찾는 문제이다.

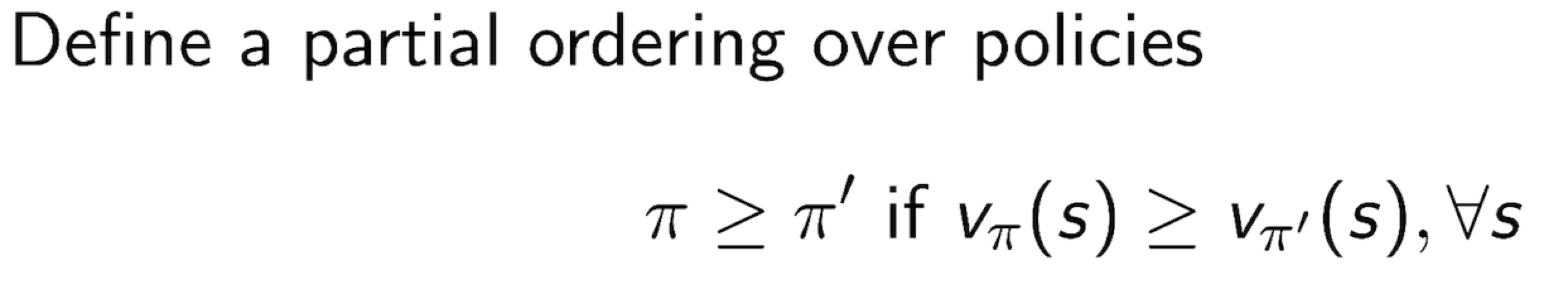
3.10 Finding an Optimal Policy

3.11 Bellman Optimality Equation for $v_{*}$

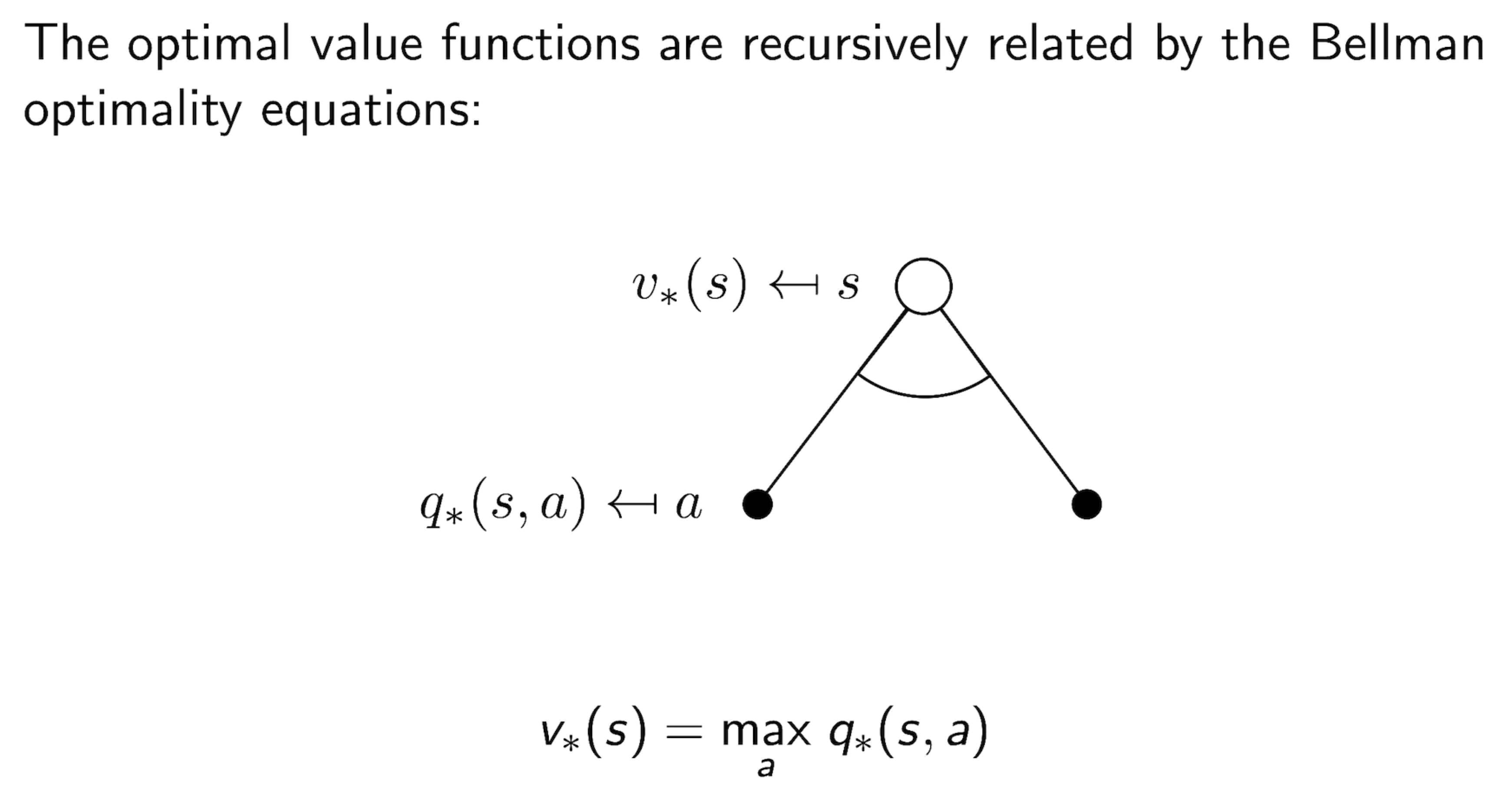
3.12 Bellman Optimality Equation for $Q^{*}$

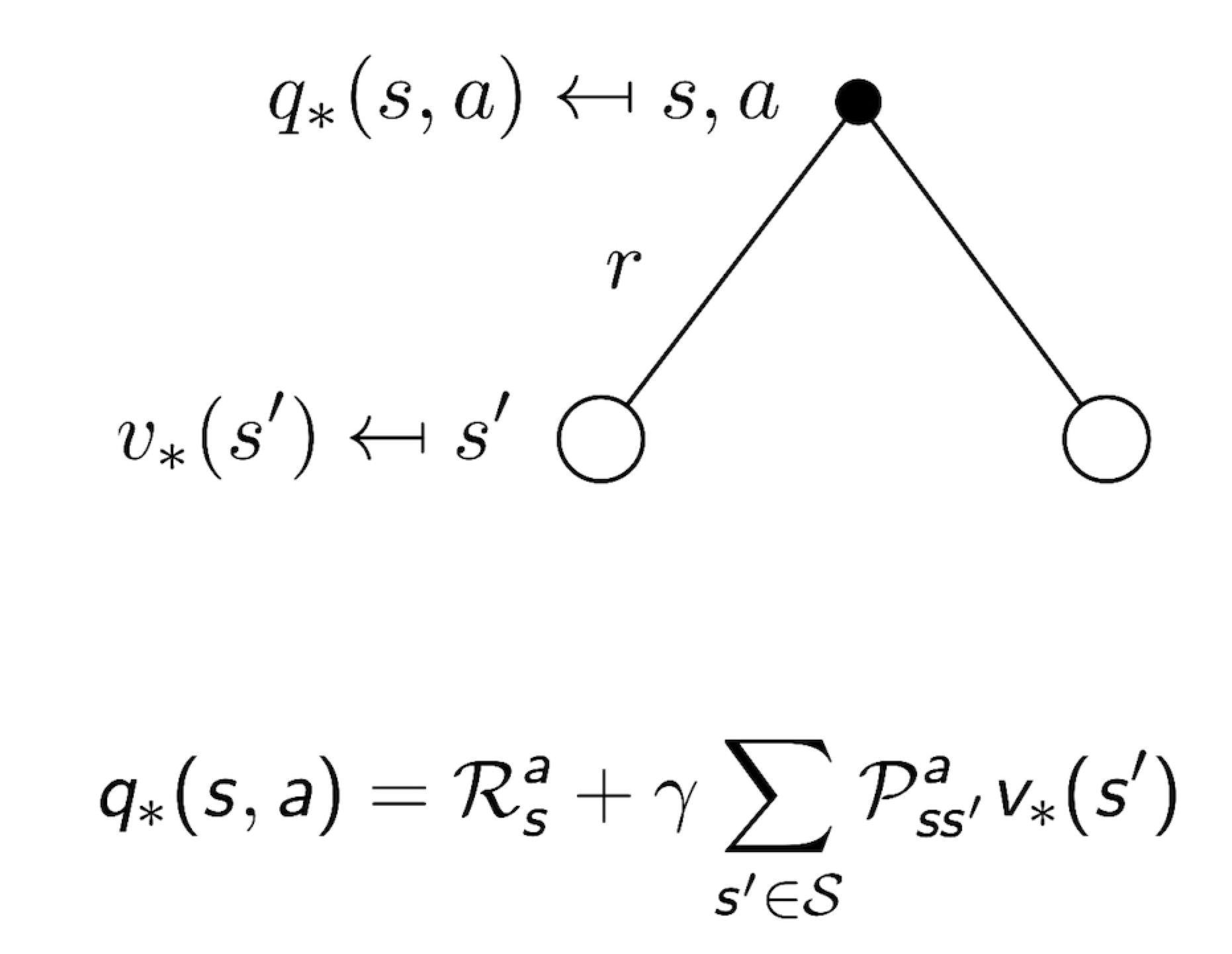
3.13 Bellman Optimality Equation for V*

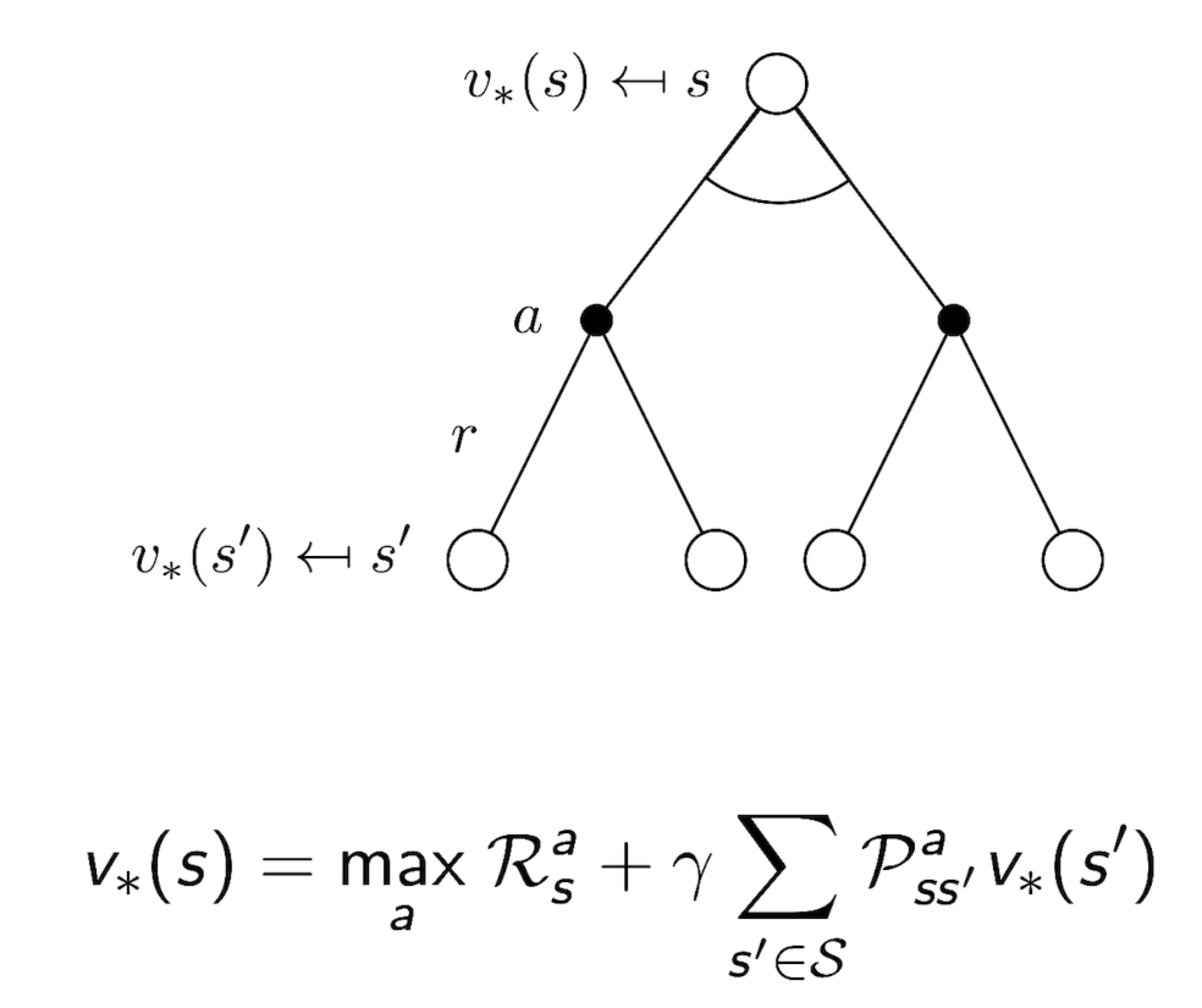
3.14 Bellman Optimality Equation for Q*

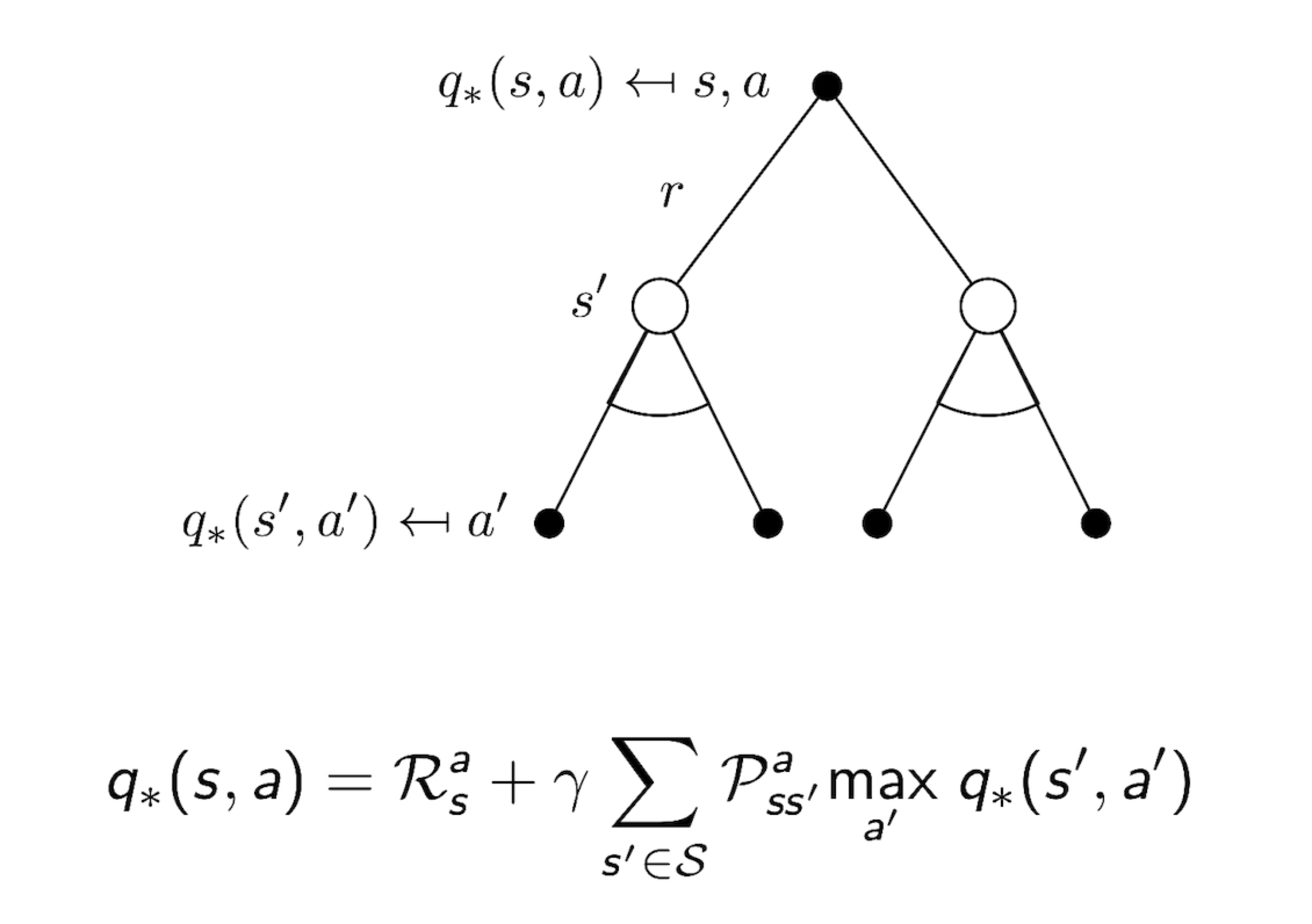
3.15 Solving the Bellman Optimality Equation

• Bellman Optimality Equation 은 Non-linear 이다
• 따라서 Closed Form Solution 이 없다
• 이 역시 iterative solution 이 그 해법
  • Value Iteration
  • Policy Iteration
  • Q-learning
  • Sarsa
• 위 solution 의 각 내용 역시, 추후 강의에서 진행되리라 기대한다.