[CS231n]Lecture04-Backprop/NeuralNetworks

Lecture 04: Backpropagation and Neural Networks

• 이 글은, Standford University 의 CS231n 강의를 듣고 스스로 정리 목적을 위해 적은 글입니다.

1. Backpropagation

1-1. 핵심

Backprop의 한줄요약: 각 parameter 에 대해 Loss Function 의 gradient 를 구하기 위해 사용하는 graphical representation of ChainRule

언뜻 보면 어려울 수 도 있지만, just ChainRule

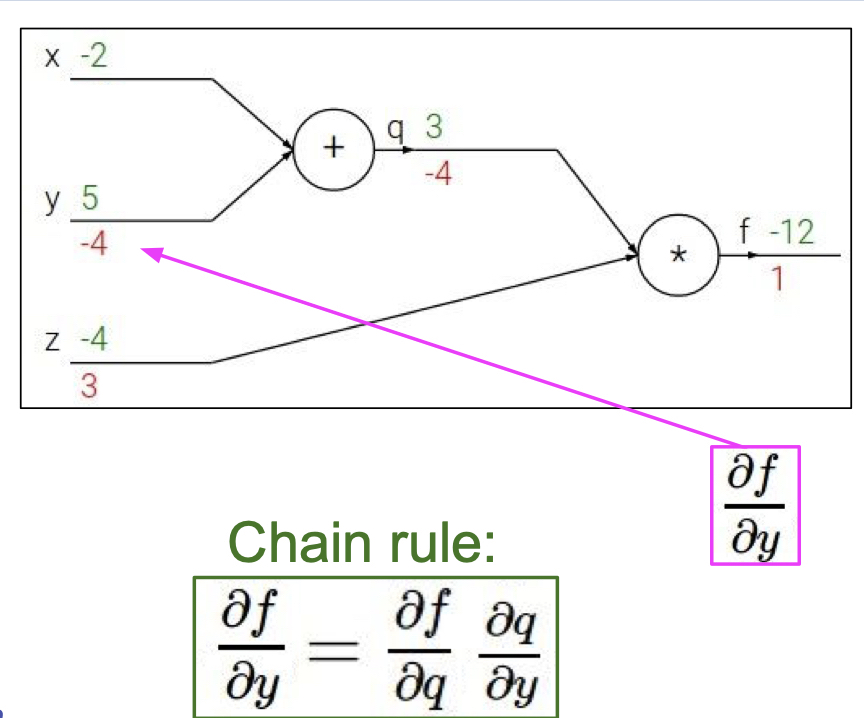
위의 그림을 예를 들어 살펴 보면, y 에 대한 f의 gradient 는 q에 대한 f의 gradient * y 에 대한 q 의 gradient 으로 볼 수 있다. 이를 해석하자면, f 에게 미치는 y 의 영향 = f 에게 미치는 q의 영향 * q 에게 미치는 y 의 영향으로 볼 수 있다.

Backpropagation 의 가장 중요한 특징!!

gradient 를 구하기 위해 node 를 기준으로 앞과 뒤만 보면 된다.

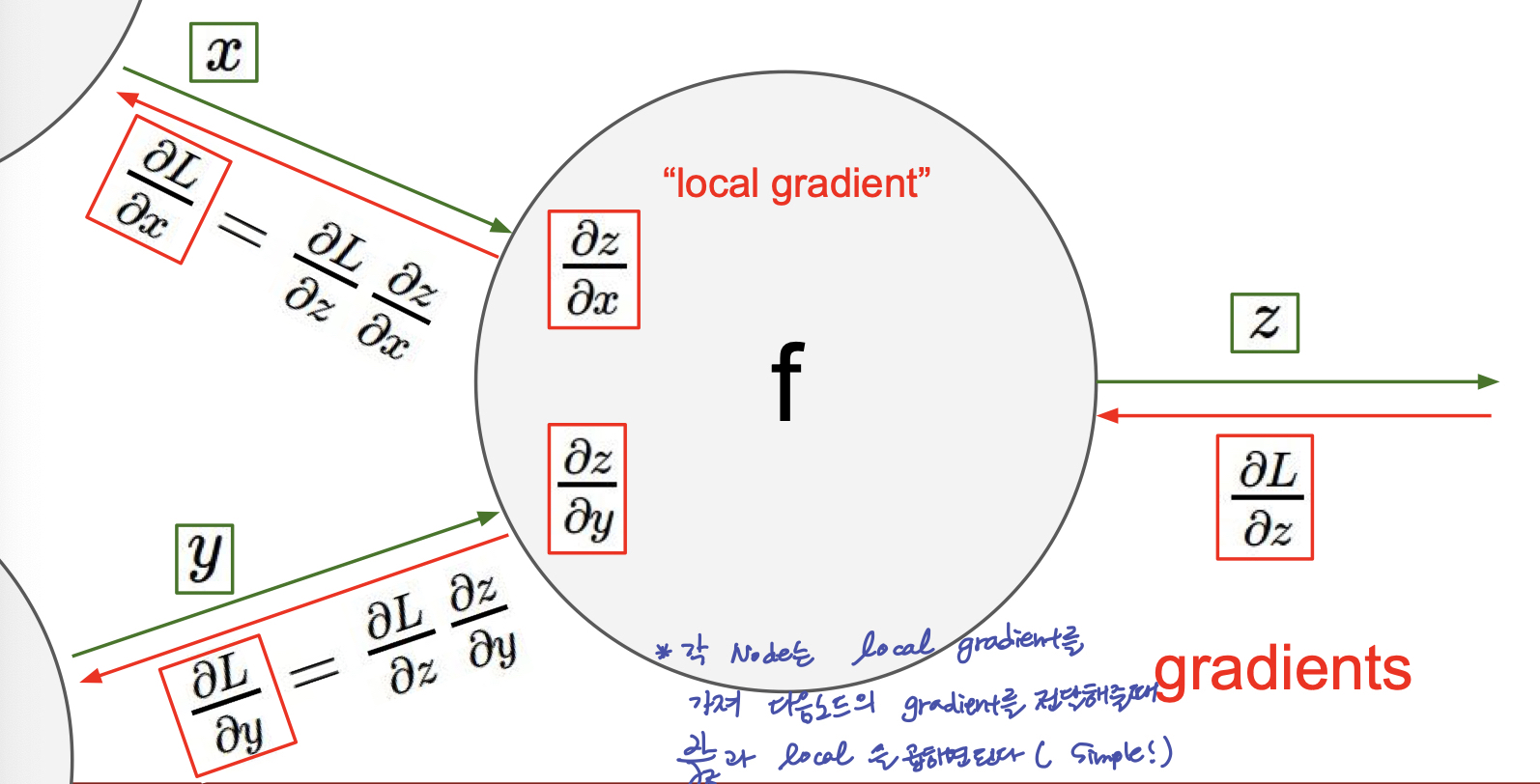
또한, 위 그림을 보게 되면, Forward passing 과 마찬가지로, Backprop 시에도, 이전 노드에서 전달 되는 Gradient 를 node 에서 local gradient 와의 연산으로 다음 Node 에 gradient 를 전달해 줄 수 있다.

1-2. Back prop 시, 각 node 의 역할

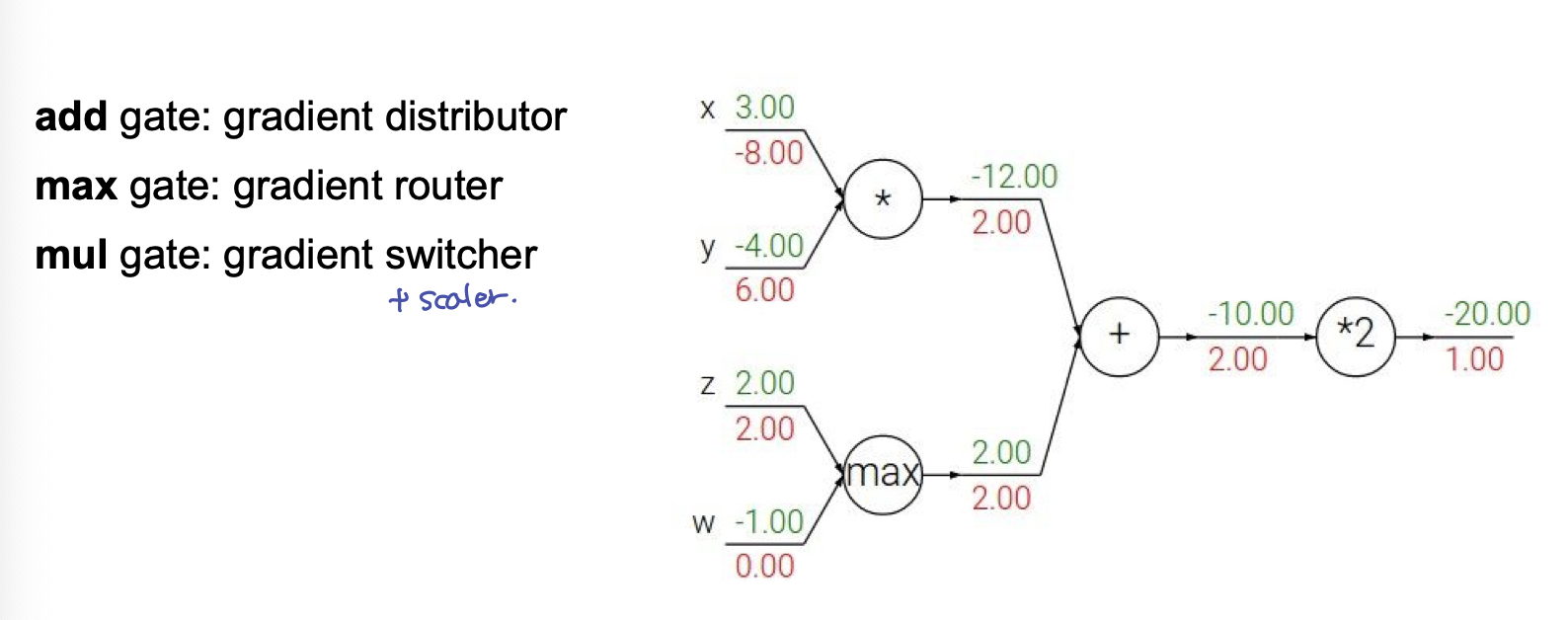
1. Add gate : gradient distributor

   • add gate 를 기점으로, 각 입력(forward 방향의 입력)의 gradient로 local gradient 를 구하면 1이므로, 전달 되는 gradient 와 각각 1씩 곱해져 전달 되게 된다. 이 현상을 보게 되면 동등하게 나눠주는 역할을 하므로 gradient distributor 라고 볼 수 있다.

2. Max gate : gradient router

   • Max gate 는 gradient 를 한쪽에는 전체, 다른 쪽에는 0 을 준다.
   • 해석적으로 보자면, max 연산을 통해 forward 방향에서 영향을 준 branch 에게 gradient 를 전달해 주는 것이 합적

   $$max(x, y) = \begin{cases} x \quad\quad if \quad x > y \\ y \quad\quad if \quad x < y \end{cases}$$

   • 수식으로 보자면, x 에 대한 gradient, y 에 대한 gradient 가 각각 (1, 0), (0, 1) 로 local gradient 가 계산되기 때문이다.
   • gradient 가 전달될 길을 결정해주는 면에서, 네트워크에서 path 를 설정해 주는 router의 기능과 비슷하다.

3. Mul gate : gradient switcher + scaler

   • 곱셈연산의 gradient 의 경우, x 에 대한 gradient 는 y 가 되므로, 서로 바꿔주는 역할을 한다. 이 때, forward 상에서의 결과 값으로 곱해주므로, scale 역할까지 함께 하게 된다.

2. Neural Networks

강의에서는 Neural Network 에 대한 intuition 을 위해, biological neuron 과 비교하였다. 모델 architecture 로서의 neuron 과 biological neuron 의 공통점은 다음과 같다.

1. input impulse
2. input axon → dendrite
3. (cell body)activation & activation function
4. output axon

이러한 비교는, 나의 개인적인 Neural Network에 대한 공부와 이해에 도움이 되지 않기에 큰 감동은 없다.

• 4강에 대한 핵심 사항은, Backpropagation 에 대한 수식적 이해와 그 이해를 통해 Backpropagation 이 gradient를 구함에 있어, 얼마나 편한 representation 인지이다. 공부하며 어려웠던 것은, backprop in vectorized 에서, Jacobian Matrix 의 표현이 scalar backprop 때와는 달리 한번에 머릿속으로 상상되지 않았기에, 손으로 써가며 따라 갔어야만 했다.

3. Reference

Lecture 4 | Introduction to Neural Networks

Syllabus | CS 231N